Hieronder vind je een aantal opgaven. Hoewel sommige vragen een correct antwoord hebben, is voor andere vragen niet direct een correct antwoord aan te wijzen. Bespreek onderling de voors en tegens van verschillende antwoorden.
Opgaven 1 t/m 6 kosten samen niet veel tijd. Opgave 7 zal de meeste tijd in beslag nemen. Voorafgaand aan opgave 7 kijk je eerst naar een kennisclip die als voorbeeld dient voor het uitvoeren van de opdracht.
Opgave 1
NHANES (National Health and Nutrition Examination survey) is een survey die sinds het begin van de jaren zestig wordt uitgevoerd door het Amerikaanse National Center for Health Statistics (NCHS). De survey verzamelt jaarlijks data over gezondheid en voeding in een steekproef van ongeveer 5.000 personen van alle leeftijden. Voor de volgende vragen wordt een subset van deze data gebruikt, bestaande uit data van volwassenen in het jaar 2011-2012.
- Welk type onderzoeksdesign is gebruikt voor het verzamelen van deze data? Experimenteel of observationeel? Motiveer je antwoord.
We
kijken eerst naar de systolische bloeddruk (SBP) van de volwassenen in
de steekproef. Hieronder staan het histogram en de boxplot van SBP
weergegeven.
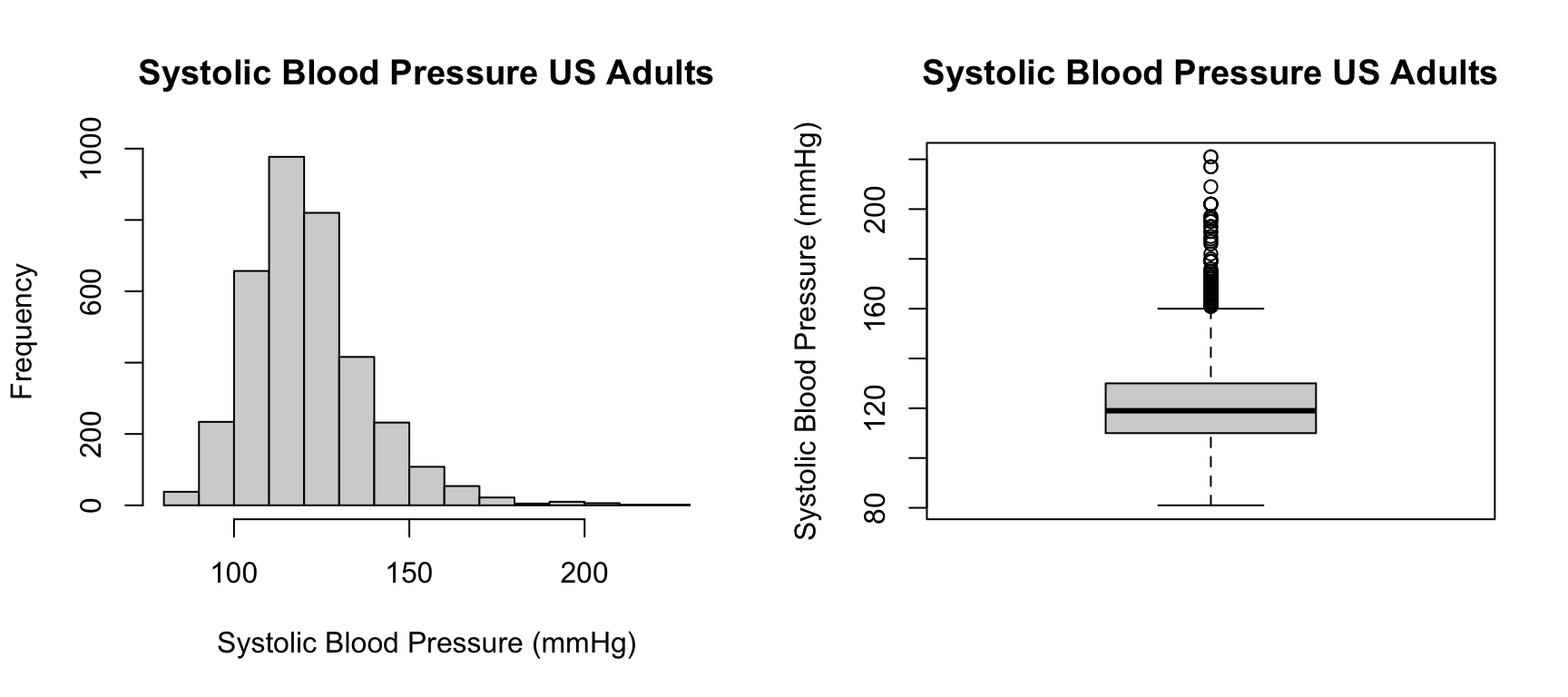
- Beschrijf de vorm van de verdeling van SBP. Welke beschrijvende statistieken zou je de voorkeur geven voor de locatie en variatie (spreiding)?
- Probeer de mediaan van SBP in de steekproef af te lezen. Wat zijn de eerste en derde kwartielen, en wat is de interkwartielafstand? Kun je schatten wat het gemiddelde en de standaarddeviatie zijn? Doe dit eerst zelf en vergelijk je antwoorden vervolgens met je groep.
Nu kijken we naar de verdeling van testosteron in de steekproef. Hieronder staan de histogram en boxplot van testosteron weergegeven.
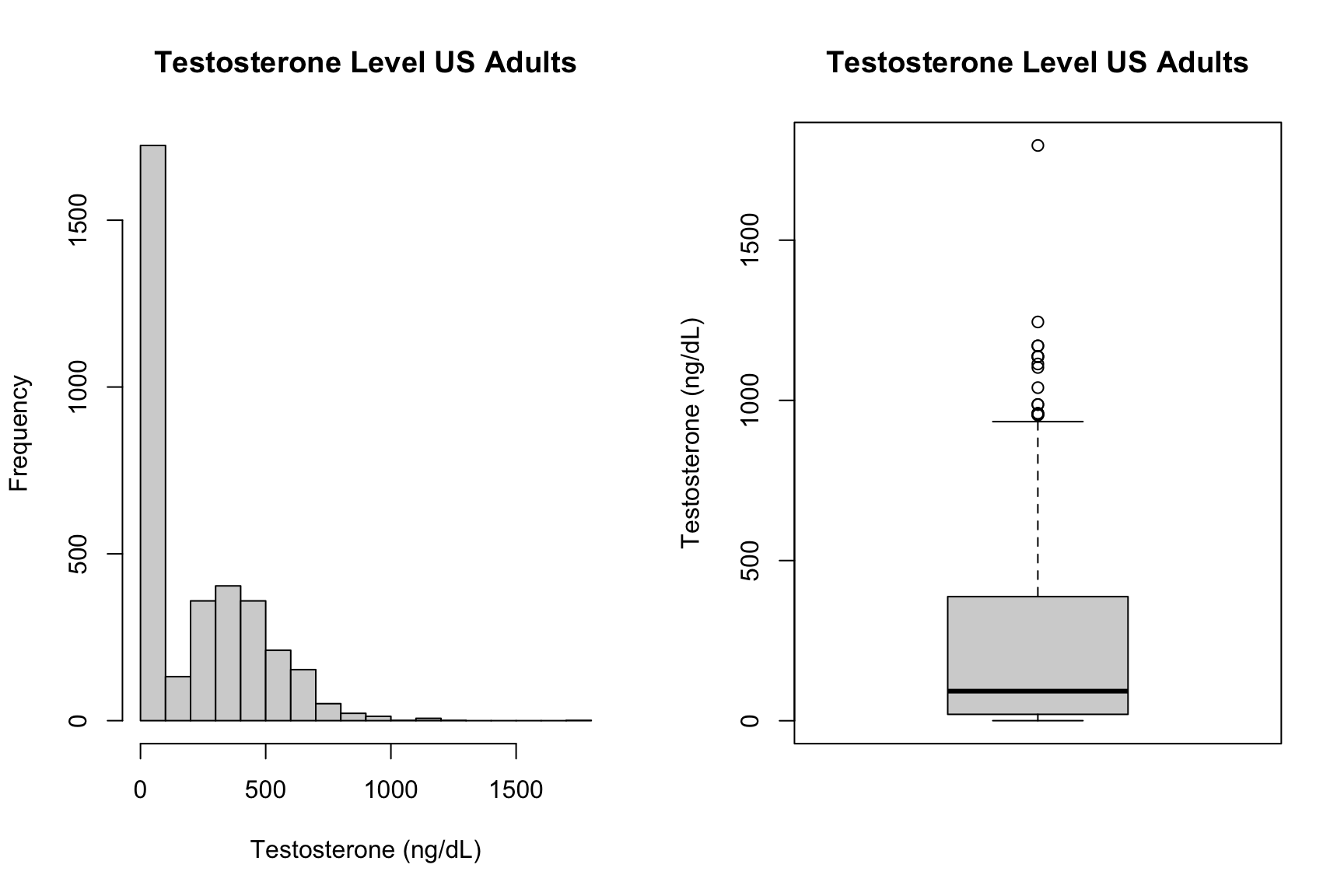
- Beschrijf wat je hier ziet. Kun je de rare verdeling verklaren? Wat is er hier waarschijnlijk misgegaan, en hoe kan dit opgelost worden?
Opgave 2
Een
arts werkt in een praktijk in de wijk Woensel-west in Eindhoven, een van
de zogenoemde Vogelaarwijken. Zij vermoedt dat er veel overgewicht is in
haar gebied, en ze heeft daarom een steekproef genomen uit haar
patiëntenbestand om dit te onderzoeken. Onderstaande histogram en
boxplot geven een overzicht van deze data. Raden jullie haar aan om het
gemiddelde of de mediaan te rapporteren in haar verslag? Ga goed na wat
de voor- en nadelen van deze beide centrummaten zijn, en maak dan een
keuze.
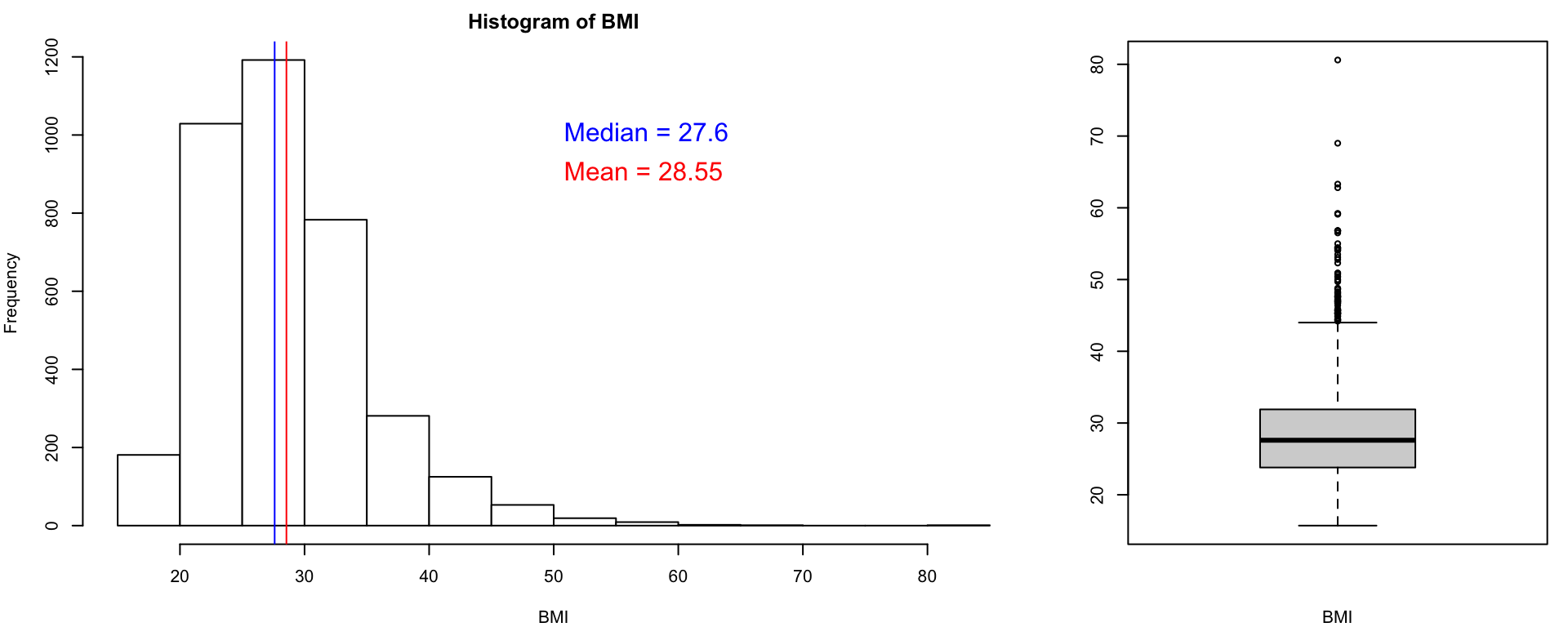
Opgave 3
Je bent gevraagd om data-analyse uit te voeren voor een presentatie op een studentencongres. Je onderzoekt serum miRNA expressie in 3 cellijnen m.b.v. TaqMan kwantitatieve PCR. Je eerste blik op de data van de eerste cellijn levert het histogram hiernaast op. Twee vrij hoge metingen vallen je op. Je checkt meteen of er fouten zijn gerapporteerd in het logboek, en je vraagt dit ook nog na, maar je vindt geen duidelijke reden voor deze afwijkingen. Wat doe je? Ga je deze uitbijters verwijderen uit je dataset, of laat je ze erin?
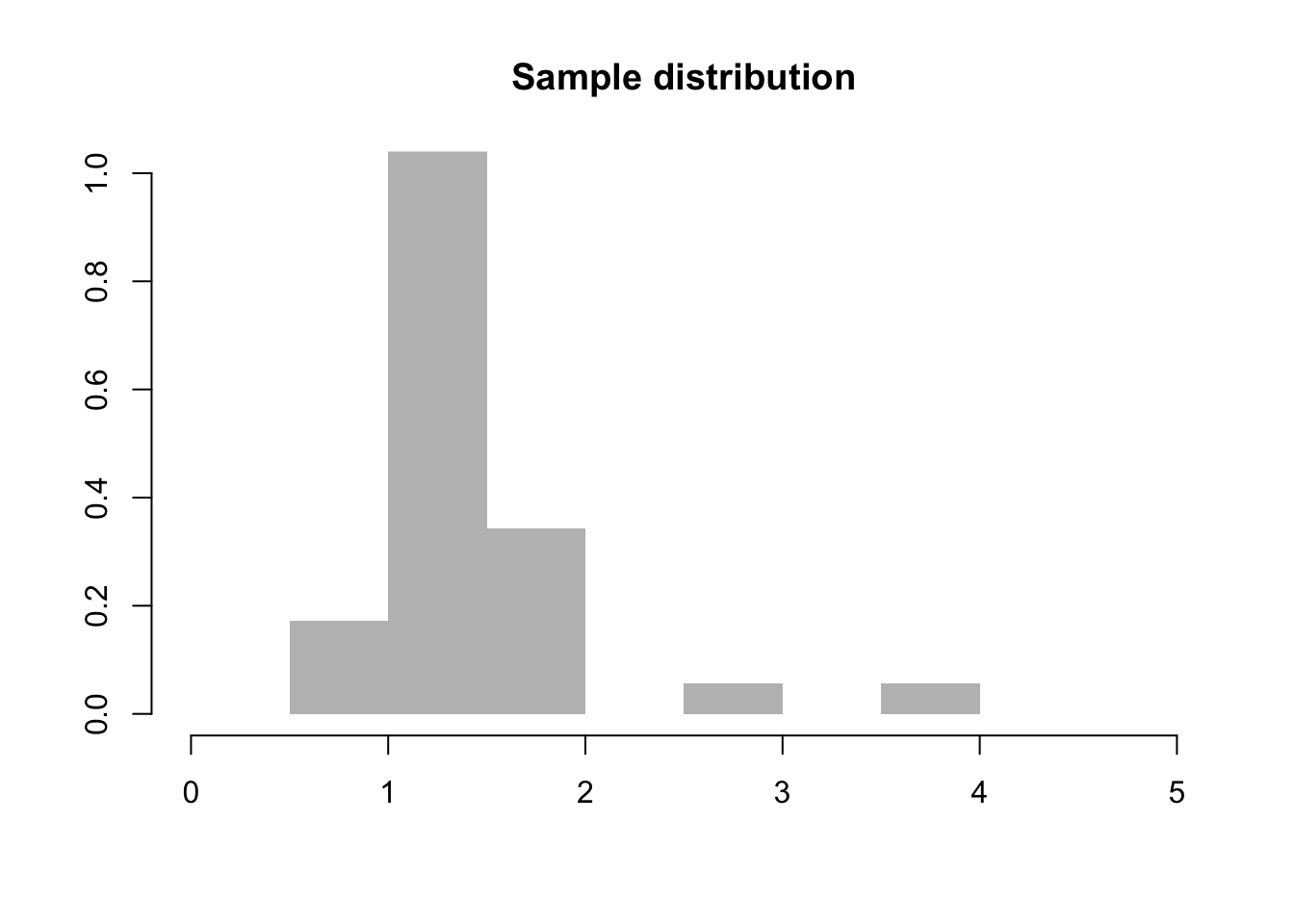
Opgave 4
Al jaren kampt 25% van de Nederlanders in de leeftijd van 30 t/m 70 jaar met een te hoog cholesterol. Je vermoedt dat dit tijdens de coronacrisis groter is geworden, en zoekt naar evidentie op dat gebied. Een collega heeft gehoord dat je die informatie zoekt en vertelt over een recente studie waarin ze hebben gevonden dat 30% van de deelnemers nu een te hoog cholesterolgehalte heeft. “Maar het was wel een kleine studie”, vertelt hij je, “Ik zal het je mailen”. Je maakt je nu zorgen dat het onderzoek weinig overtuigend zal zijn. 30% is meer dan 25%, maar als deze studie heel erg klein is?
Hoeveel deelnemers wil jij in deze studie zien om overtuigd te raken van een afwijkende waarde? Je mag hier af gaan op je intuïtie. In de tabel hieronder staan een aantal voorbeelden van verhoudingen tussen totaal aantal deelnemers en deelnemers met een verhoogd cholesterol.
| Totaal aantal | Aantal verhoogd | percentage |
|---|---|---|
| 6 | 2 | 33% |
| 10 | 3 | 30% |
| 20 | 6 | 30% |
| 50 | 15 | 30% |
| 100 | 30 | 30% |
| 200 | 60 | 30% |
| 400 | 120 | 30% |
| 800 | 240 | 30% |
We maken in opgaven 5 en 6 gebruik van de NHANES dataset, die al eerder aan bod is gekomen. Het betreft een grote, observationele studie van volwassenen in de Verenigde Staten. In de dataset staan variabelen over demografische kenmerken, leefstijl, voeding, en de gezondheidstoestand van ongeveer 5000 deelnemers.
Opgave 5
Verschillende variabelen kunnen vergeleken worden tussen rokers, niet rokers en voormalig rokers. Er waren 2027 personen die niet meer dan 100 sigaretten gerookt hebben, 698 personen roken nog steeds (>100 sigaretten in totaal), en 862 personen zijn gestopt (voormalig >100 sigaretten in totaal). 120 personen hebben geen antwoord gegeven.
We vergelijken nu de systolische bloeddruk (SBP, systolic blood pressure) van de drie groepen (afbeelding hieronder). Geef antwoord op de volgende vragen:
- Verhoogt roken de systolische bloeddruk?
- Hebben voormalig rokers een hogere systolische bloeddruk dan niet-rokers?
![Chart, box and whisker chart
Figuur 1.
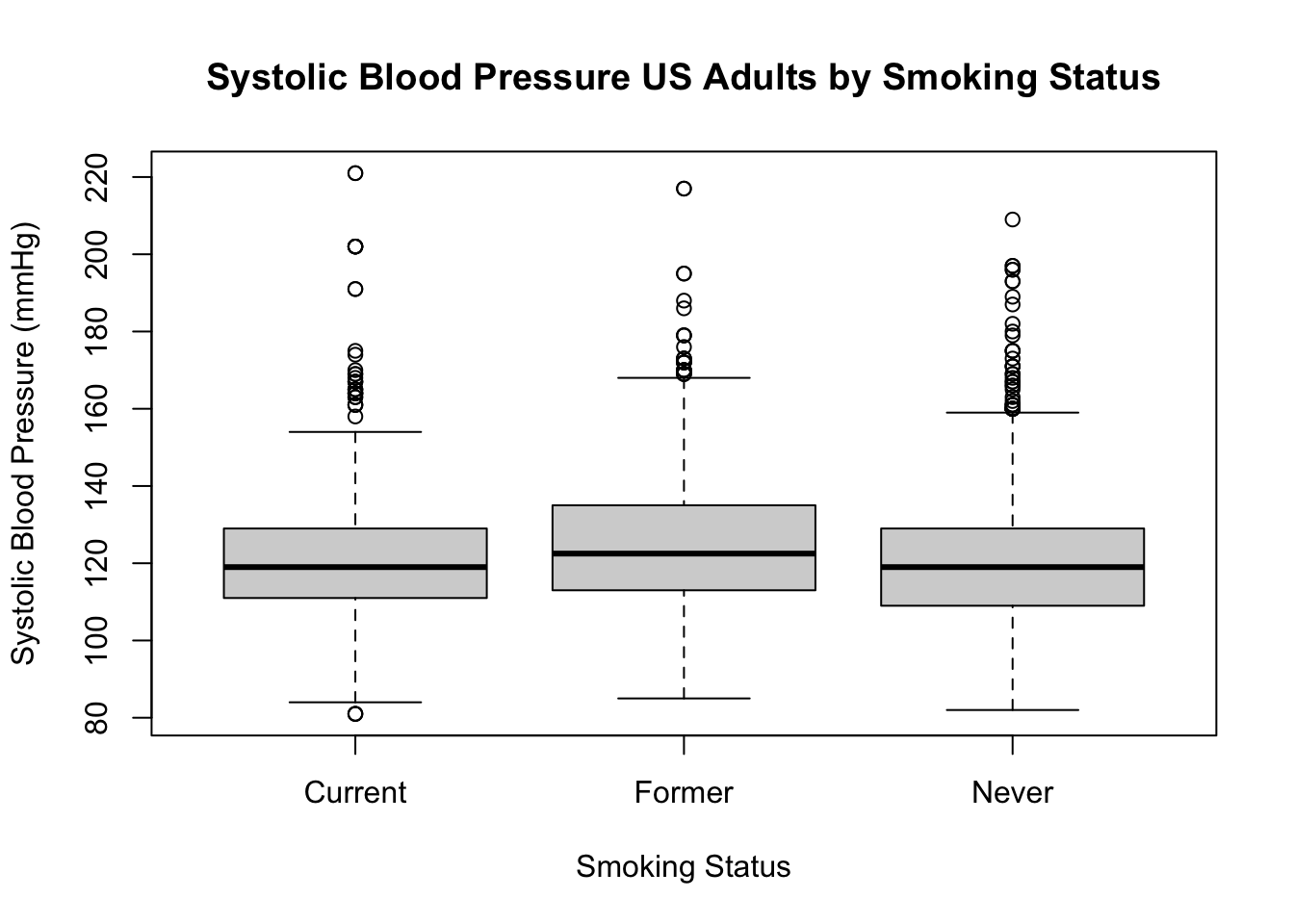
- Wat voor verdeling zien we in de afbeelding hierboven?
- Denk je dat er verschillen zijn in SBP voor de 3 groepen? Waarom wel/niet?
Opgave 6
In de NHANES dataset is HDL cholesterol gegeven in mmol/L. Dit is in veel landen de standaard eenheid van HDL cholesterol, in tegenstelling tot de VS. Daar wordt de eenheid mg/dL gebruikt, hiervoor is de conversie factor om van mmol/L naar mg/dL te transformeren 38.61004.
- Voor een Amerikaanse collega moeten de volgende componenten worden omgerekend: mean, median, standard deviation en IQR naar mg/dL.
n mean sd min max range IQR Q0.25 Q0.5 Q0.75
3500 5 1.06 1.53 12.28 10.75 1.4 4.24 4.91 5.64
![Chart, histogram
Figuur 2.
Ook is er besproken hoe bepaalde transformaties kunnen helpen met scheve verdelingen (skewed distributions). De bovenstaande afbeelding is de directe/absolute HDL cholesterol. De verdeling is rechts-scheef (“right skewed”), zoals veel andere lab/fysische meetbare variabelen. Vaak is het handiger om een (ongeveer) normaal verdeelde uitkomst variabele te hebben. Een veelvoorkomende transformatie is de natuurlijke log-transformatie (ln), waar ook log10 of log2 kan werken. Welke log gebruikt wordt hangt af van de context, in dit geval is er geen overduidelijke reden om een andere log dan ln te gebruiken. Hier onder zien we de distributie van de getransformeerde HDL cholesterol.
![Chart, histogram
Figuur 3.
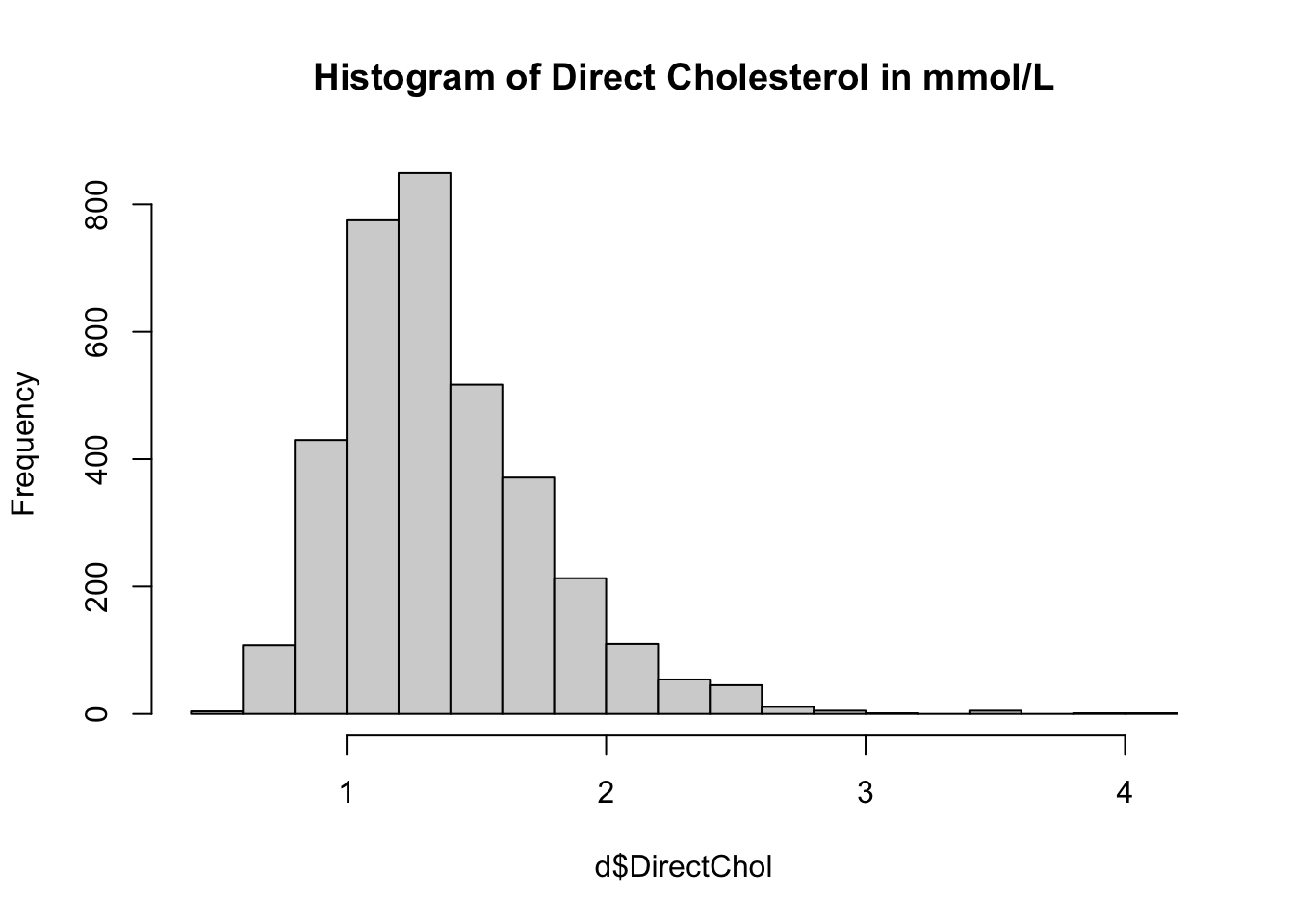
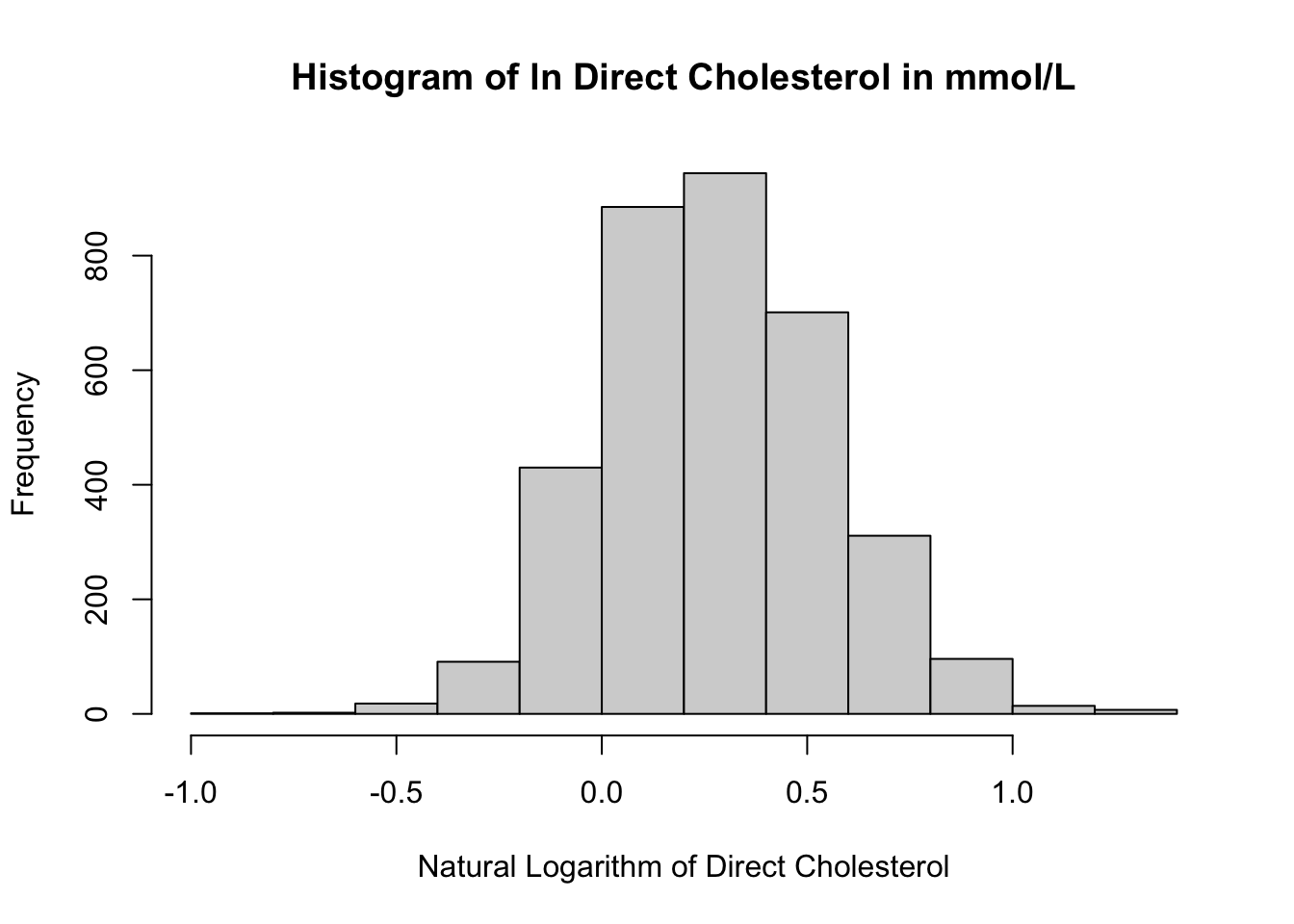
- Wat is er aan de distributie veranderd?
Opgave 7
In deze opgave vragen we jullie om informatie uit een krant kritisch te evalueren. Je doet dit door het oorspronkelijke artikel op te zoeken en daarvan in ieder geval het abstract en de figuren en tabellen goed van te bekijken en vergelijken met het krantenartikel. Docenten en onderwijsassistenten kunnen jullie nog een aantal specifieke vragen stellen.
- Kies één van de volgende vijf krantenartikelen en lees het goed door (als je klaar bent en je genoeg tijd hebt dan kun je nog een tweede kiezen):
- Malaria/ ventilatiebuis
- Alzheimer / slaap
- Krant: https://news.yahoo.com/sleeping-less-6-hours-night-140339287.html
- Oorspronkelijke artikel: https://www.nature.com/articles/s41467-021-22354-2
- Diagnose met pleister
- Krant: https://www.deingenieur.nl/artikel/pleister-meet-met-zweet-je-gezondheid
- Oorspronkelijke artikel: https://advances.sciencemag.org/content/5/1/eaav3294
- Obesitas en Covid-19 / pfizer vaccin
- Malaria / vaccin
- Kijk nu naar het eerste deel (tot 5:25) van de volgende kennisclip (statistical literacy 2020 – deel 2):
https://video.uu.nl/permalink/v126896cf432fqhet224/iframe/
- Ga nu aan de slag met je eigen krantenartikel. Beantwoord in ieder
geval onderstaande vragen en geef ook aan waar die informatie te vinden
is: in het wetenschappelijke artikel? In het krantenartikel?
- Welke onderzoeksvraag wil men met dit onderzoek beantwoorden?
- Wat is de onderzoekspopulatie?
- Op welke manier is de steekproef samengesteld en hebben de onderzoekers hiermee een representatieve steekproef voor de onderzoekspopulatie?
- Welk onderzoeksdesign wordt hier gebruikt?
- Wat is de uitkomstmaat?
- Welke beschrijvende statistieken over de participanten worden gerapporteerd?
- Wat is volgens jou de conclusie die je op basis van dit onderzoek kunt trekken?
- Geven de nieuwsberichten de resultaten correct weer?
- Zijn er nog andere dingen die je opgevallen zijn in het krantenartikel of het wetenschappelijke artikel?