Werkcollege Leereenheid 2: Correlaties en het lineaire model

Introductie

Maak de opgaven hieronder in je werkgroep. Je mag ook in je eentje werken, maar bij vragen en onduidelijkheden is het verstandig om eerst met je groep te overleggen. Je leert namelijk het meest door elkaar te bevragen en dingen aan elkaar uit te leggen.

Leerdoelen

De student:

kan samenvattingen van steekproefdata interpreteren
herkent dat de context bepaalt welke keuzes gemaakt kunnen en moeten worden m.b.t. statistiek
heeft inzicht in de geïnformeerde keuzes die gemaakt worden in statistische databeschrijving en analyse

Opgave 1

De gestelde onderzoeksvraag: Hebben mensen met een hoger gewicht, een hogere bloeddruk? Om dit te onderzoeken analyseren we de relatie tussen BMI (continue, numerieke variabele) en SBP (continue, numerieke variabele). In de afbeelding hieronder zijn de twee variabelen tegen elkaar uitgezet.

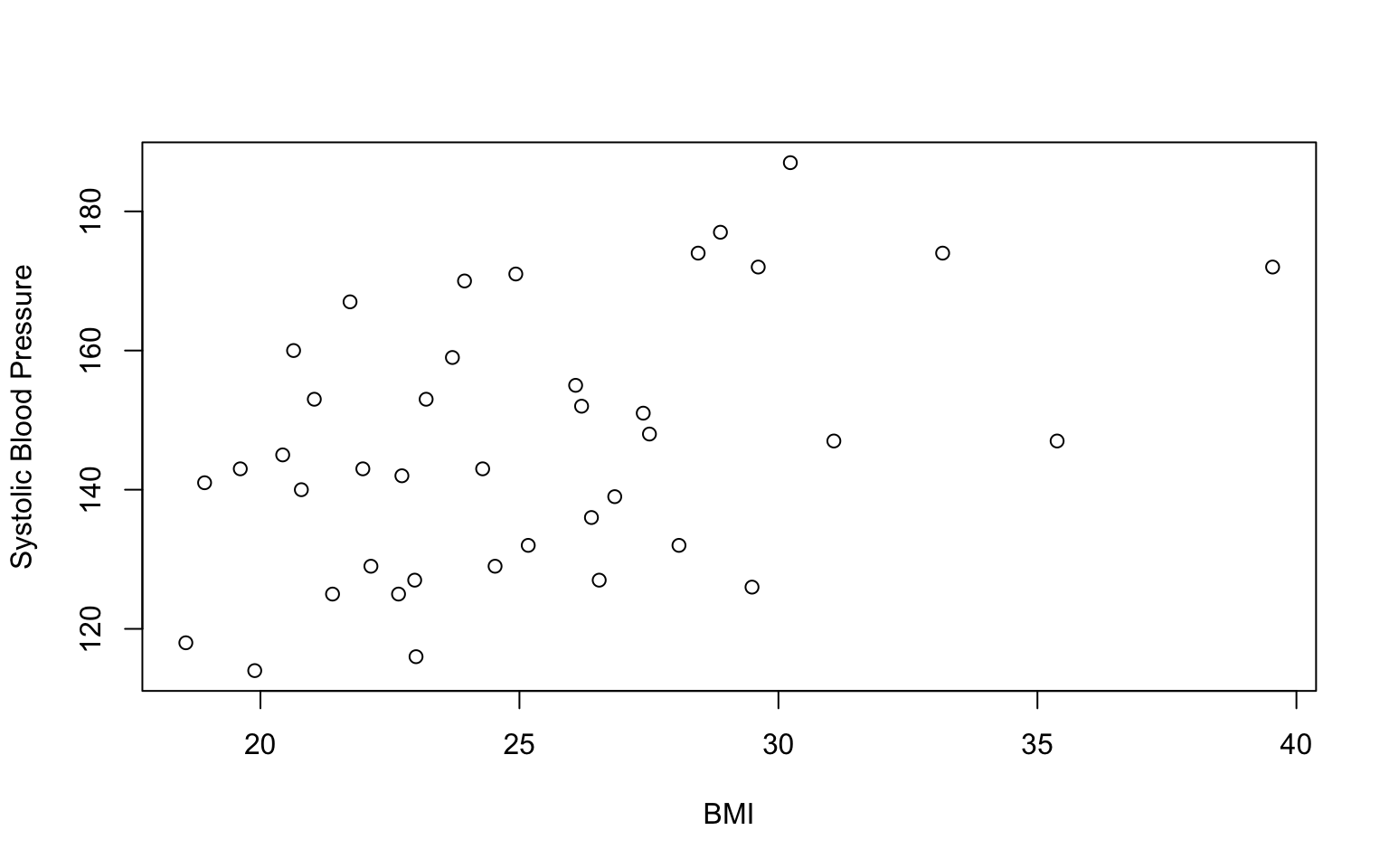
Hoe zou je de relatie tussen BMI en SBP karakteriseren? Als je denkt dat er een correlatie is, hoe sterk is deze dan?

Opgave 2

Stel dat je thesisbegeleider je vraagt om het verband tussen overgewicht en bloeddruk te onderzoeken. Geef je de data dan weer in een spreidingsdiagram (scatterplot), twee boxplots of een 2x2 tabel (zie hieronder)? Wat zijn de voor- en nadelen van deze data-samenvattingen? Beantwoorden ze dezelfde onderzoeksvraag?

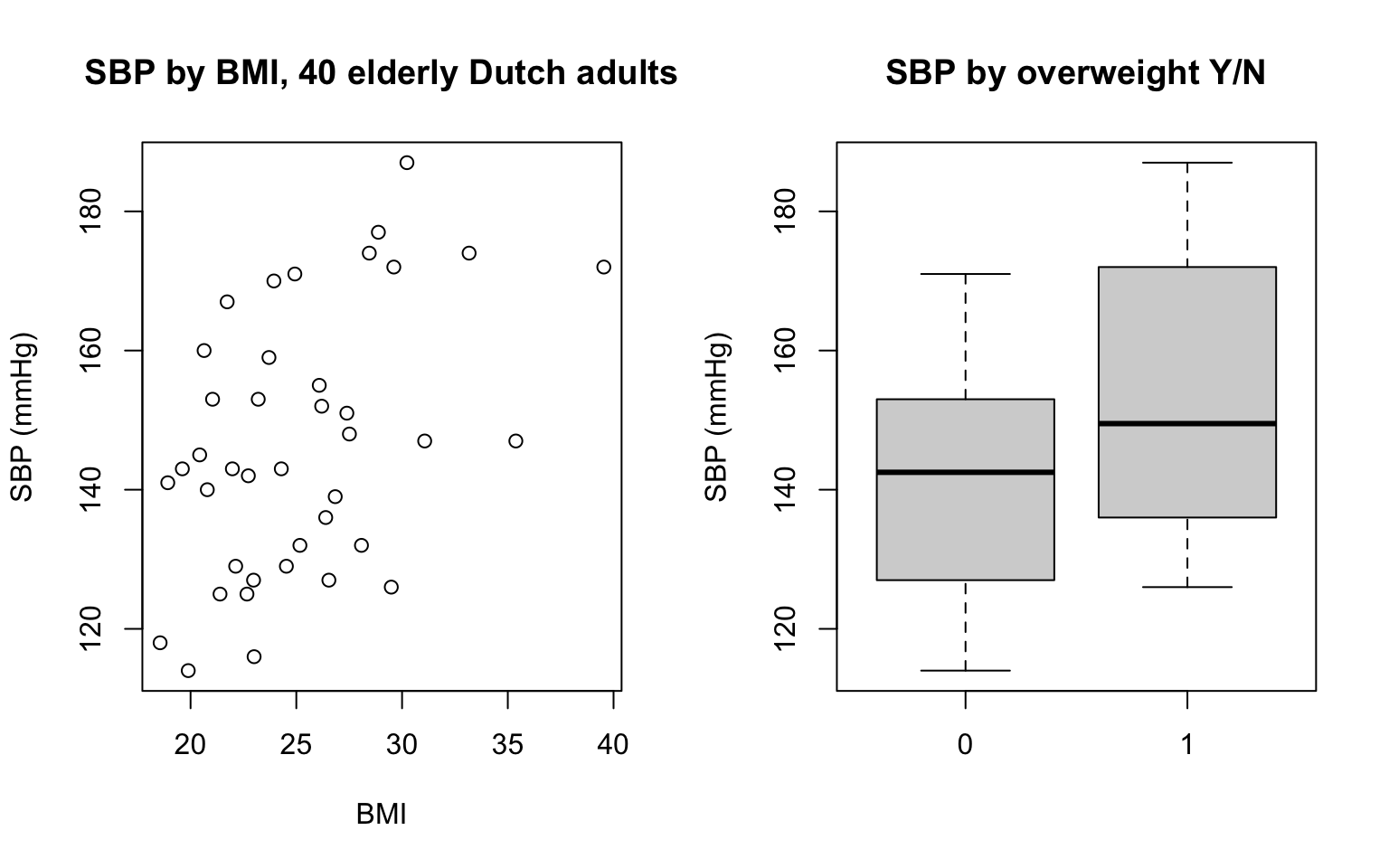
	Geen hypertensie	Wel hypertensie	Totaal
Geen obesitas	15 (68%)	7 (32%)	22
Wel obesitas	9 (50%)	9 (50%)	18
Totaal	24	16	40

Opgave 3

In onderstaand spreidingsdiagram is het aantal kindersterftegevallen per duizend levendgeborenen (mort) afgezet tegen het aantal baby’s van tienermoeders per duizend zwangerschappen (teen).

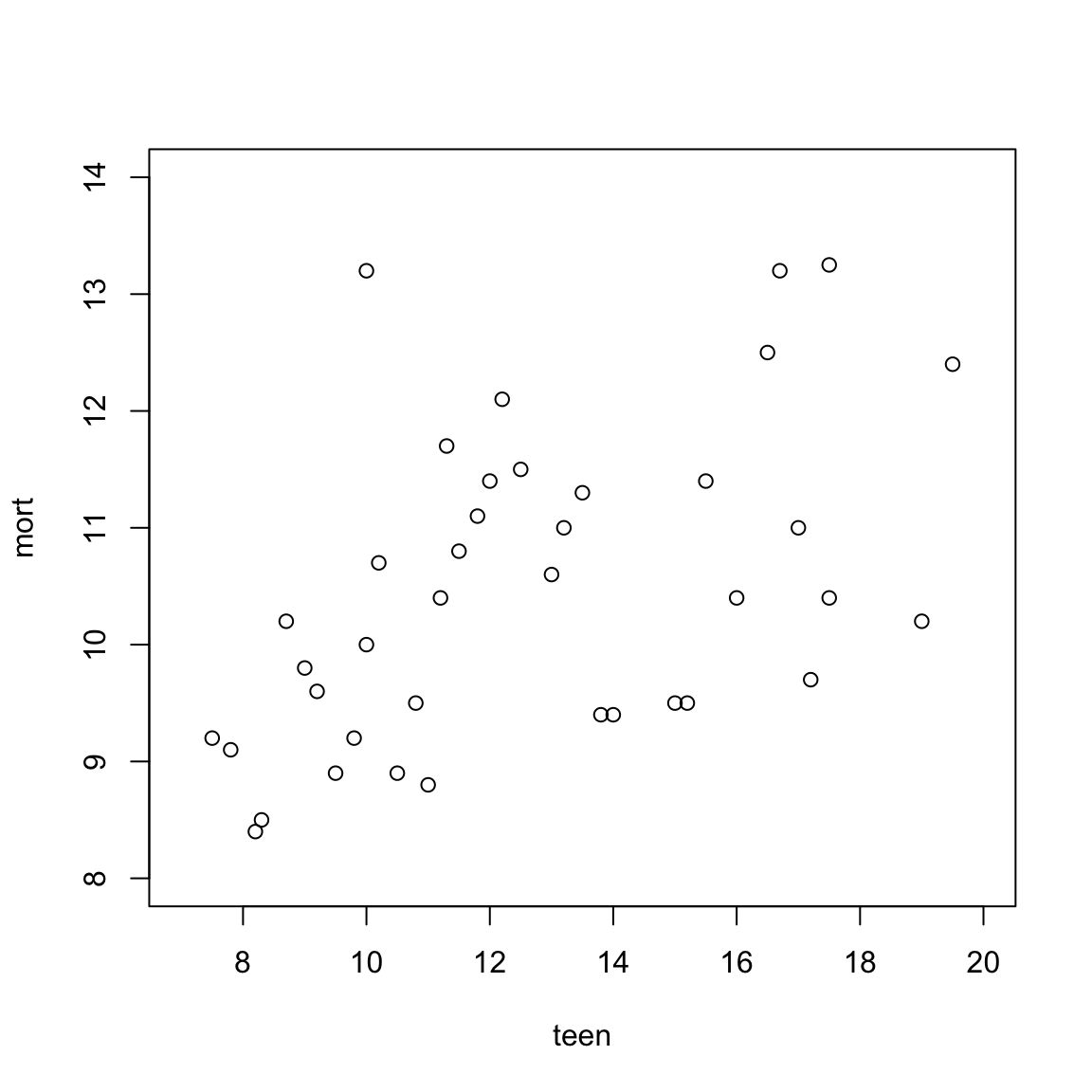
Wat lees je af uit het spreidingsdiagram over de relatie tussen kindersterfte en tienermoederschap?
De correlatie tussen kindersterfte en tienermoederschap is 0.4823176. Hoeveel variantie in kindersterfte wordt dan verklaard door tienermoederschap?

Hieronder dezelfde figuur nogmaals, met de regressielijn erin.

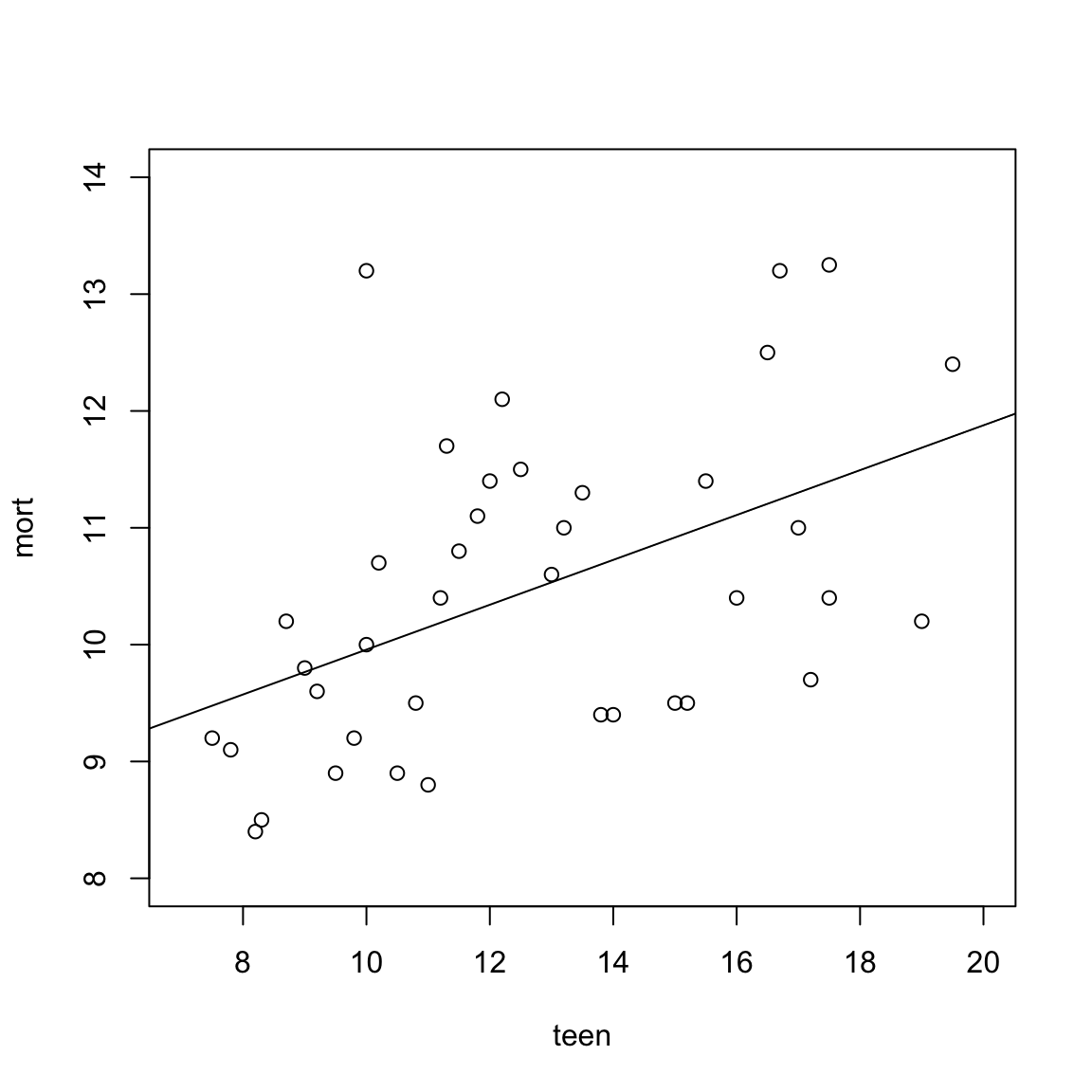
Geef zo op het zicht een schatting van de hellingshoek-regressiecoëfficiënt. Leg daarbij uit hoe je tot die schatting komt.

(Een deel van) de lineaire regressie analyse in R van kindersterfte op tienermoederschap geeft de volgende output.

## 
## Call:
## lm(formula = mort ~ teen)
## 
## Coefficients:
## (Intercept)         teen  
##      8.0368       0.1921

Stel de vergelijking van de regressielijn op.
Wat betekent een regressiecoëfficiënt van 0.19?
Geef een voorspelling voor de gemiddelde kindersterfte wanneer de het aantal tienermoeders per duizend zwangerschappen gelijk is aan 12.
Stel dat het aantal tienermoeders per duizend zwangerschappen door overheidsmaatregelen verlaagd wordt naar 4 per duizend zwangerschappen, wat is dan de verwachte gemiddelde kindersterfte?
Een statisticus zegt dat je voorzichtig moet zijn met de conclusie uit g. Kun je zelf redenen bedenken waarom zij dat zegt?

Opgave 4

Onderzoekers zijn geïnteresseerd naar invloed van leeftijd op systolische bloeddruk. De interesse gaat in het bijzonder uit naar mannen tussen de 32 en de 42 jaar, aangezien uit eerder onderzoek is gebleken dat deze groep een verhoogd risico heeft op een te hoge systolische bloeddruk. De onderzoekers hebben daarom besloten een (random) steekproef te trekken van mannen in deze leeftijdsgroep en hebben voor iedere man de leeftijd en het gemiddelde van drie metingen van de systolische bloeddruk genoteerd. Deze observaties hebben ze vervolgens afgebeeld in een scatterplot (figuur 6).

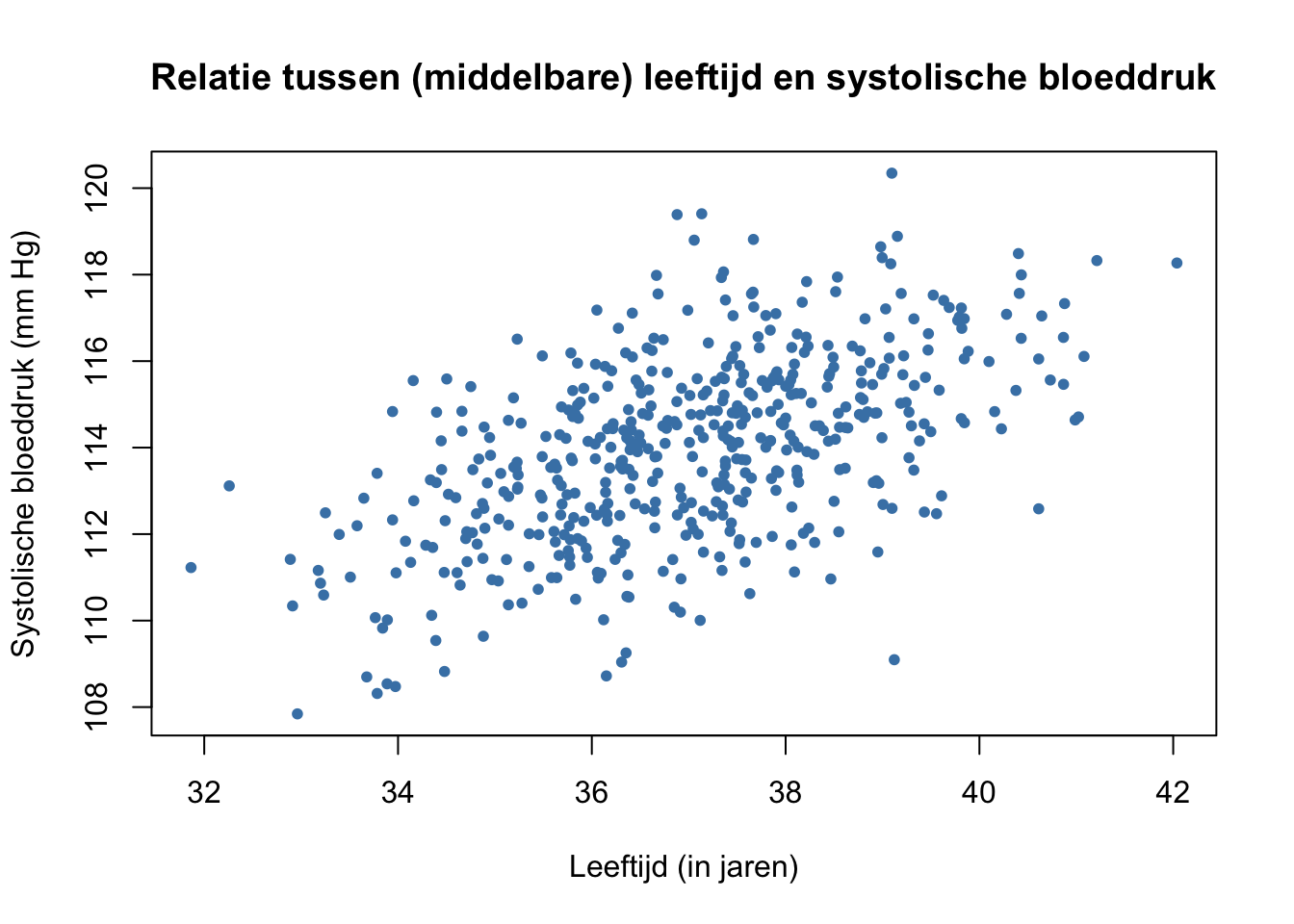
Hoe sterk schat je de correlatie tussen leeftijd en systolische bloeddruk in de bovenstaande figuur?
Kun je aan de hand van de figuur 6 iets zeggen over de systolische bloeddruk van alle mannen tussen de 32 en de 42 jaar? Waarom wel/niet?
Zijn er uitbijters die de correlatie sterk beïnvloeden?
Doe het volgende eerst individueel, en vergelijk dan jullie antwoorden met elkaar:
1. Trek op het oog een regressielijn door deze puntenwolk.
2. Schat vervolgens op basis van je lijn hoe groot de gemiddelde systolische bloeddruk van 33-jarige mannen is.
3. Schat ook hoe groot de gemiddelde systolische bloeddruk van 37-jarige mannen is. Vergelijk deze geschatte waarden vervolgens met de waarden van je medestudenten.
4. Komen jullie schattingen in beide situaties overeen?
5. Zit er verschil in de spreiding van jullie schattingen voor 33- en 37-jarige mannen? Leg uit waarom dit wel of niet zo is?
Doe hetzelfde voor mannen van 26. Wijken jullie schattingen nu meer of minder af van elkaar? Is het geoorloofd om deze schatting te gebruiken?

Tijdens de onderzoeksperiode hebben de onderzoekers niet alleen leeftijd en systolische bloeddruk gemeten, maar ook de hoeveelheid thyroxine (t4) in het lichaam. De onderzoekers hebben namelijk de volgende hypothese: Hoe meer thyroxine in het lichaam, hoe hoger de systolische bloeddruk. Allereerst bekijken zij de correlatie tussen de twee variabelen (Onderstaande Figuur):

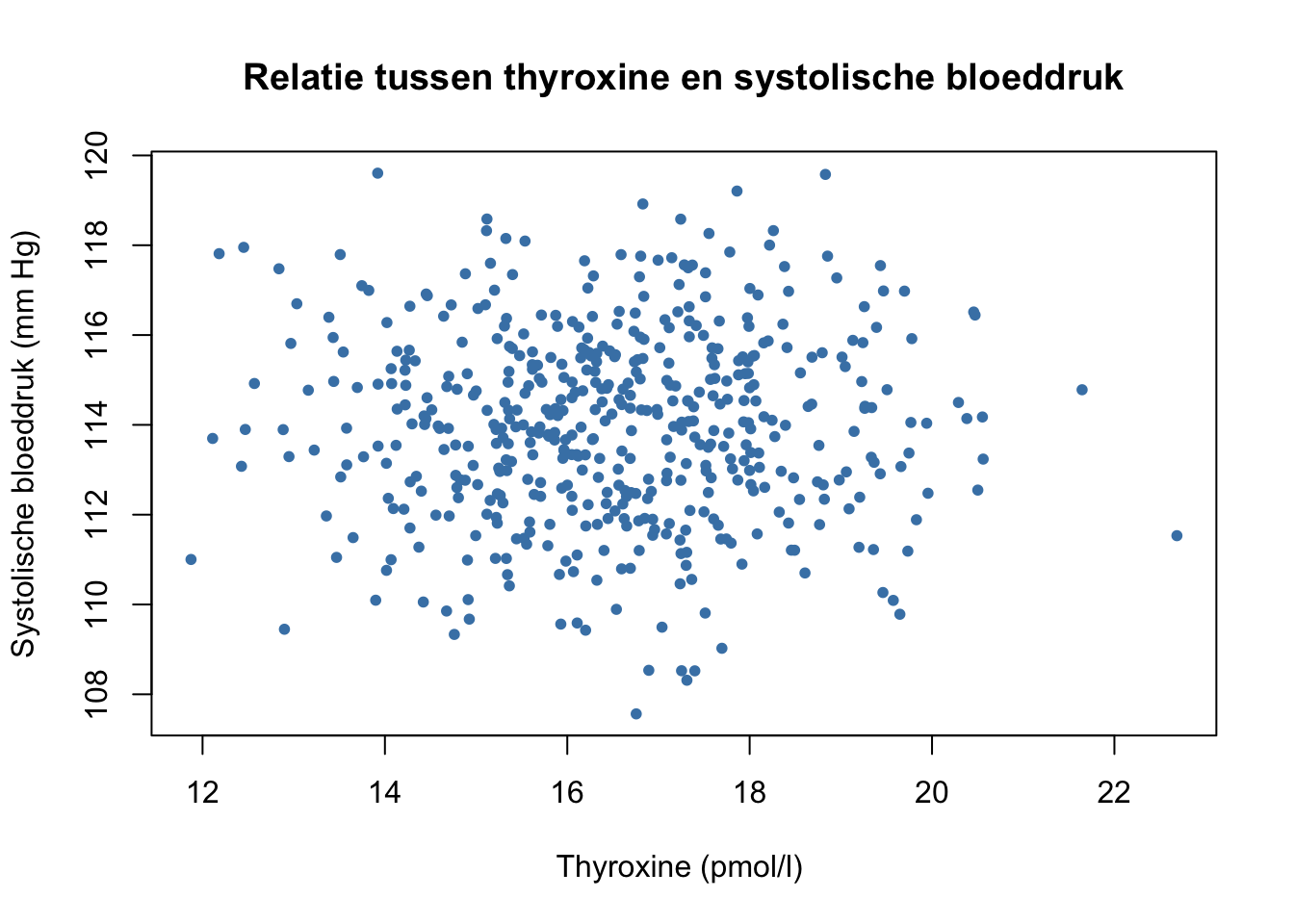
Wat kan je zeggen over de relatie tussen thyroxine en systolische bloeddruk?
Hoe sterk schat je de correlatie tussen thyroxine en systolische bloeddruk?

Opgave 5

We zijn geïnteresseerd in de relatie tussen twee variabelen, X en Y. Bekijk de eerste drie spreidingsdiagrammen die hieronder zijn afgebeeld (A, B en C) en beantwoord de volgende vragen.

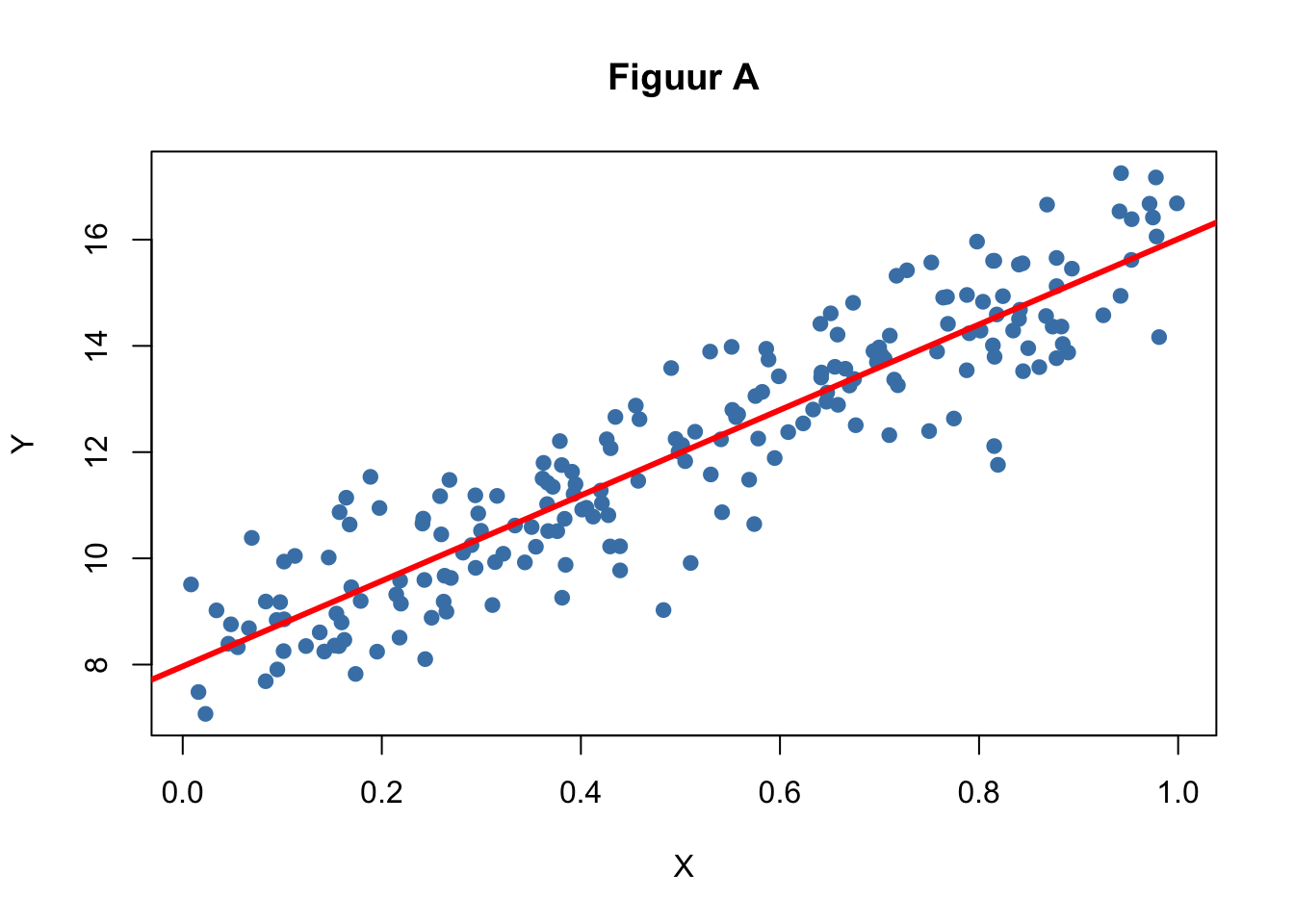
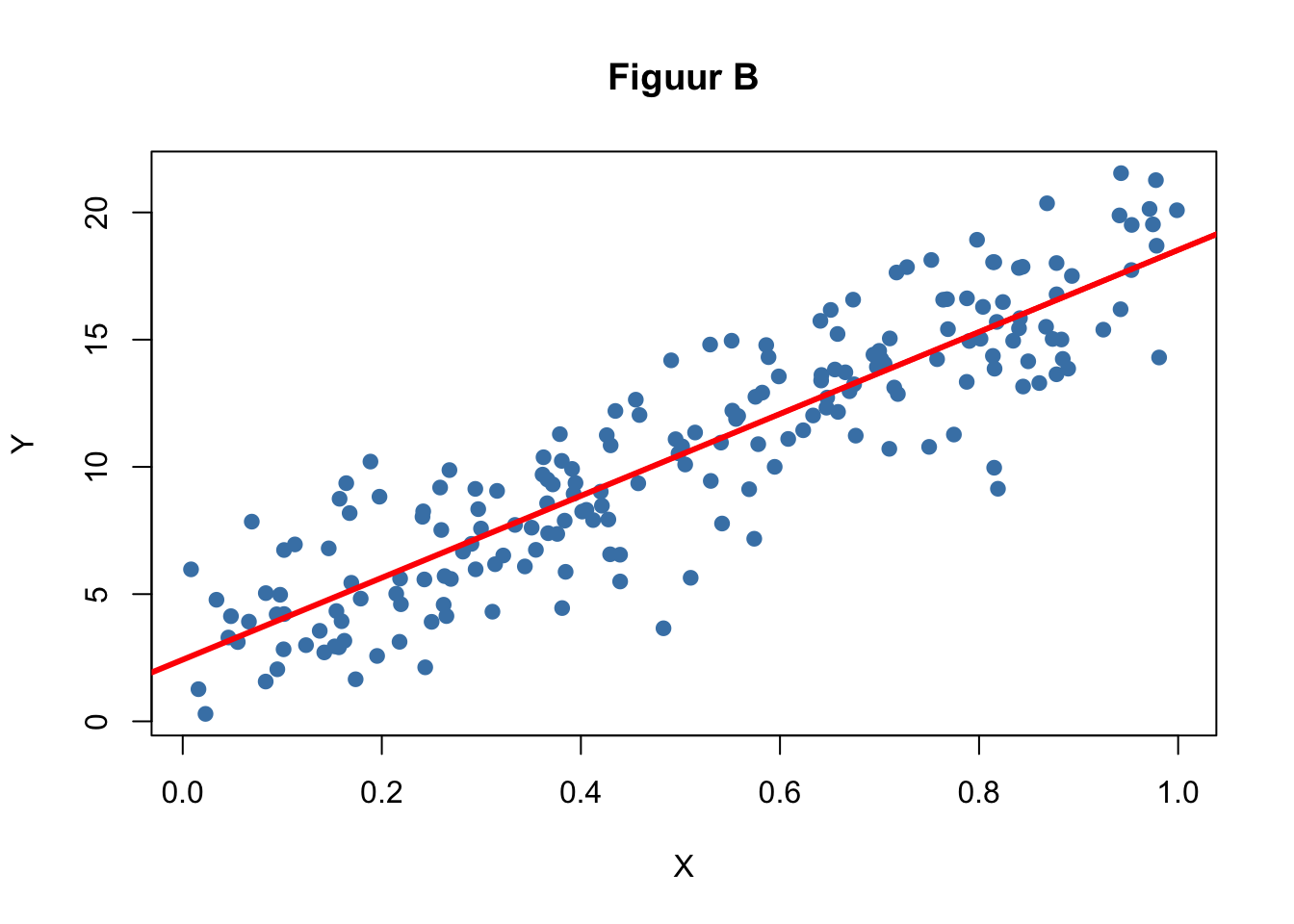
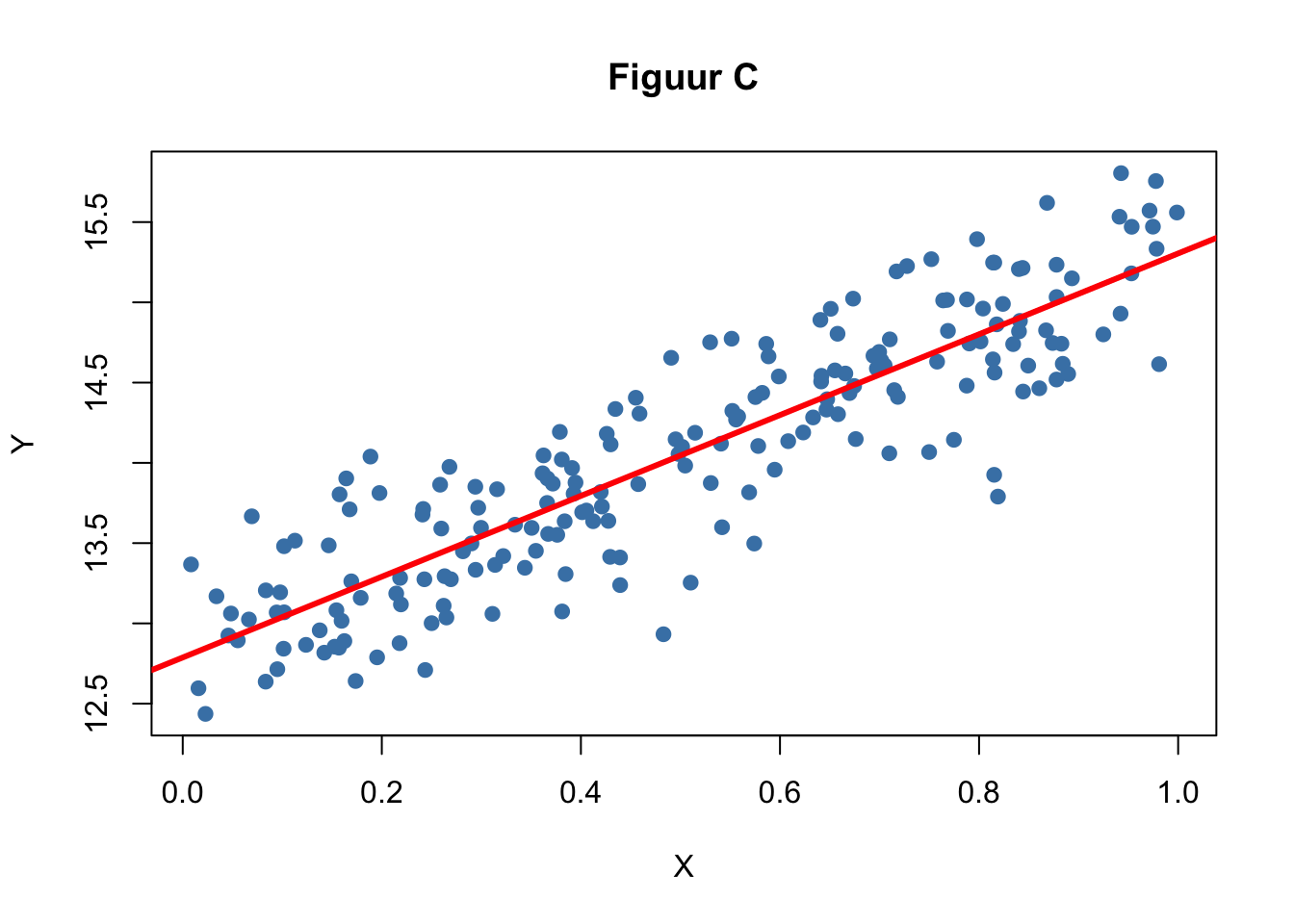
Vergelijk de figuren met elkaar. Wat is de overeenkomst en wat zijn de verschillen?
Schat de correlatiecoëfficiënten voor de drie figuren.
Bereken op basis van je schatting de determinatiecoëfficiënten.
Bepaal zo goed mogelijk de hellingshoeken voor alle drie de figuren. Wat is de betekenis van de hellingshoek?
Noteer de intercept voor elk van de drie figuren. Wat is de betekenis van de intercept?
Wat gebeurt er met de intercept als je een iets andere hellingshoek hebt geschat?
Wat gebeurt er met de regressiecoëfficiënt als je afdwingt dat de regressielijn door het punt (0,0) moet gaan, en de intercept dus 0 is?
Beantwoord nu dezelfde vragen (3a tm 3e) voor de volgende 3 figuren (D, E en F):

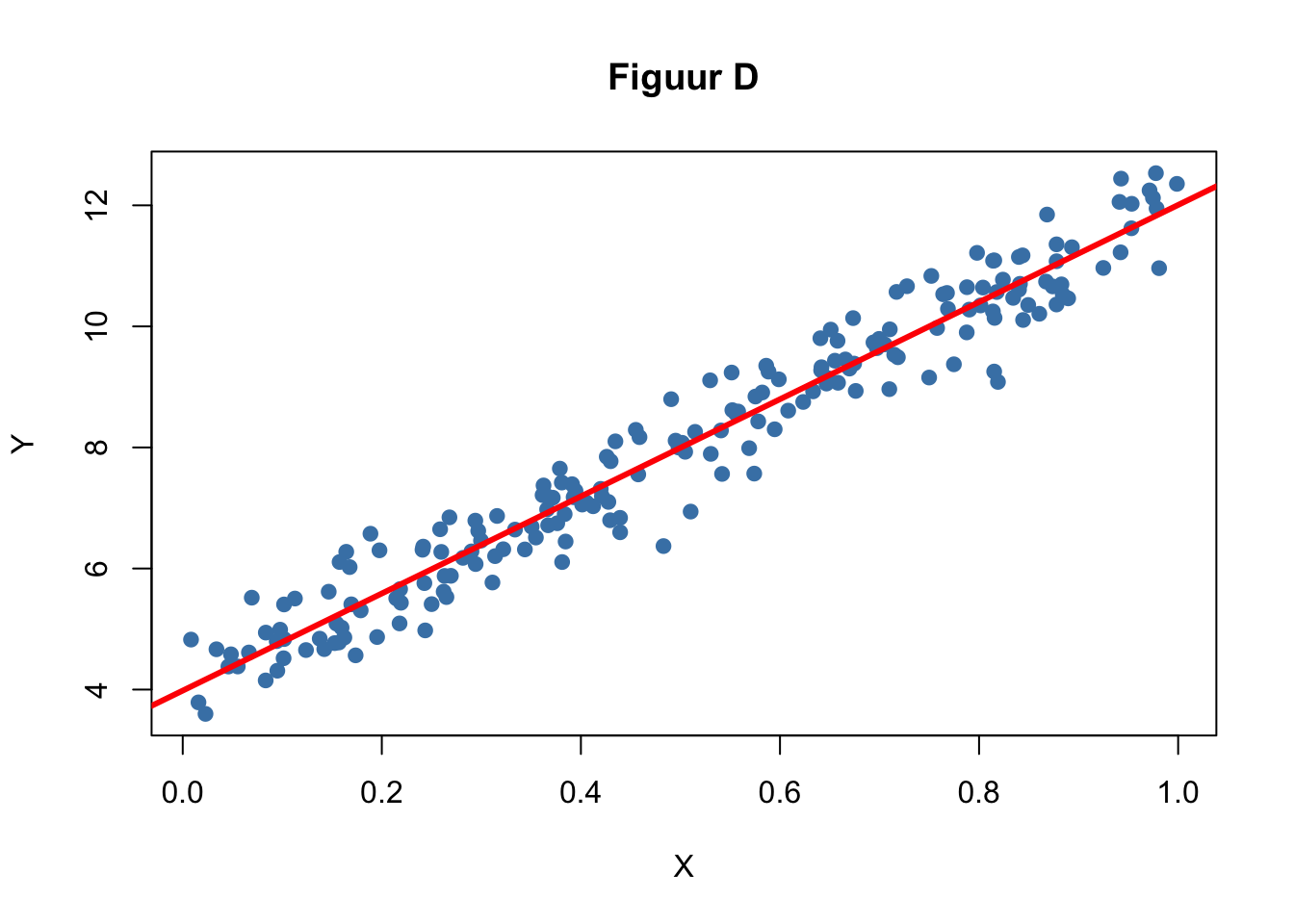
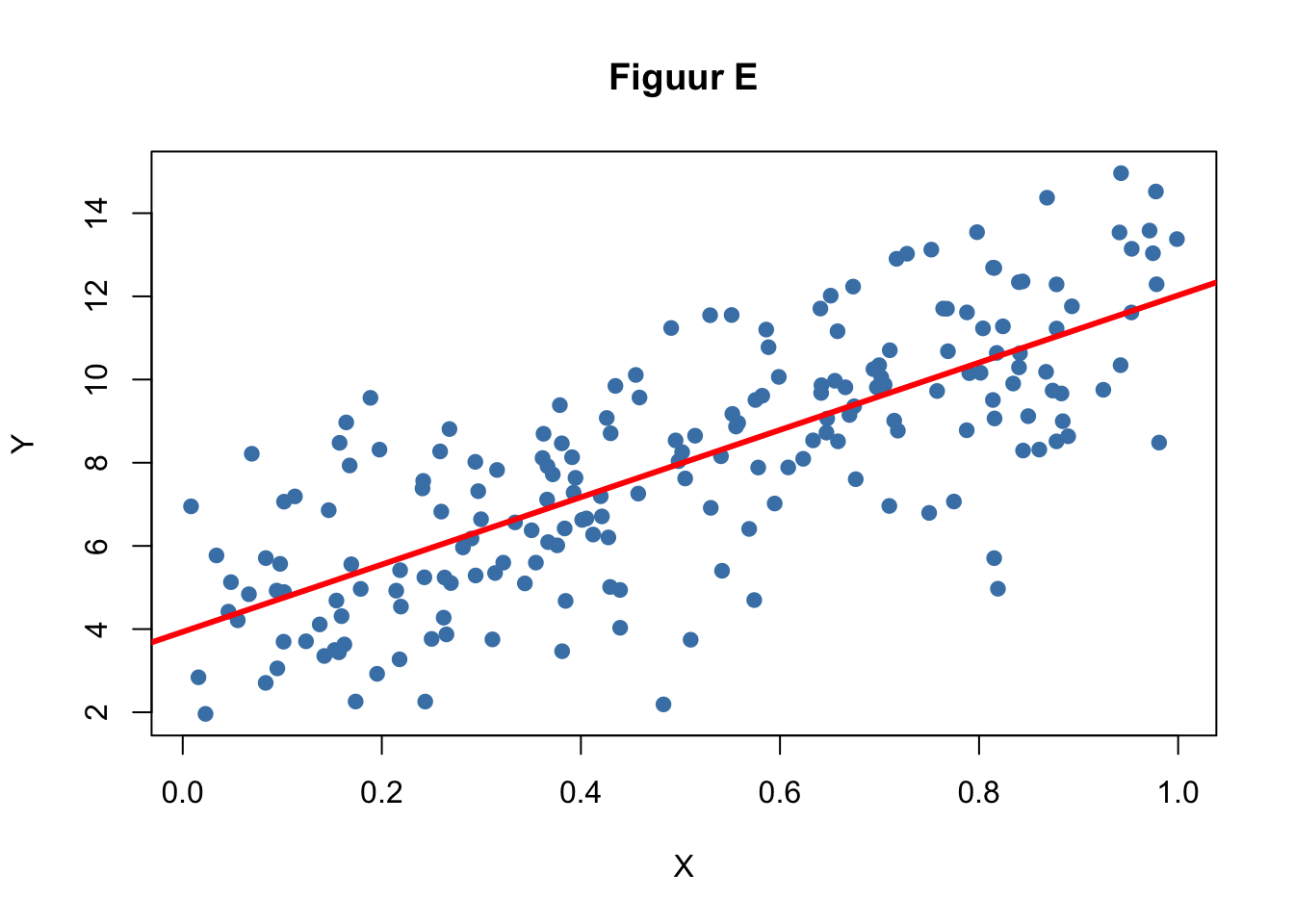
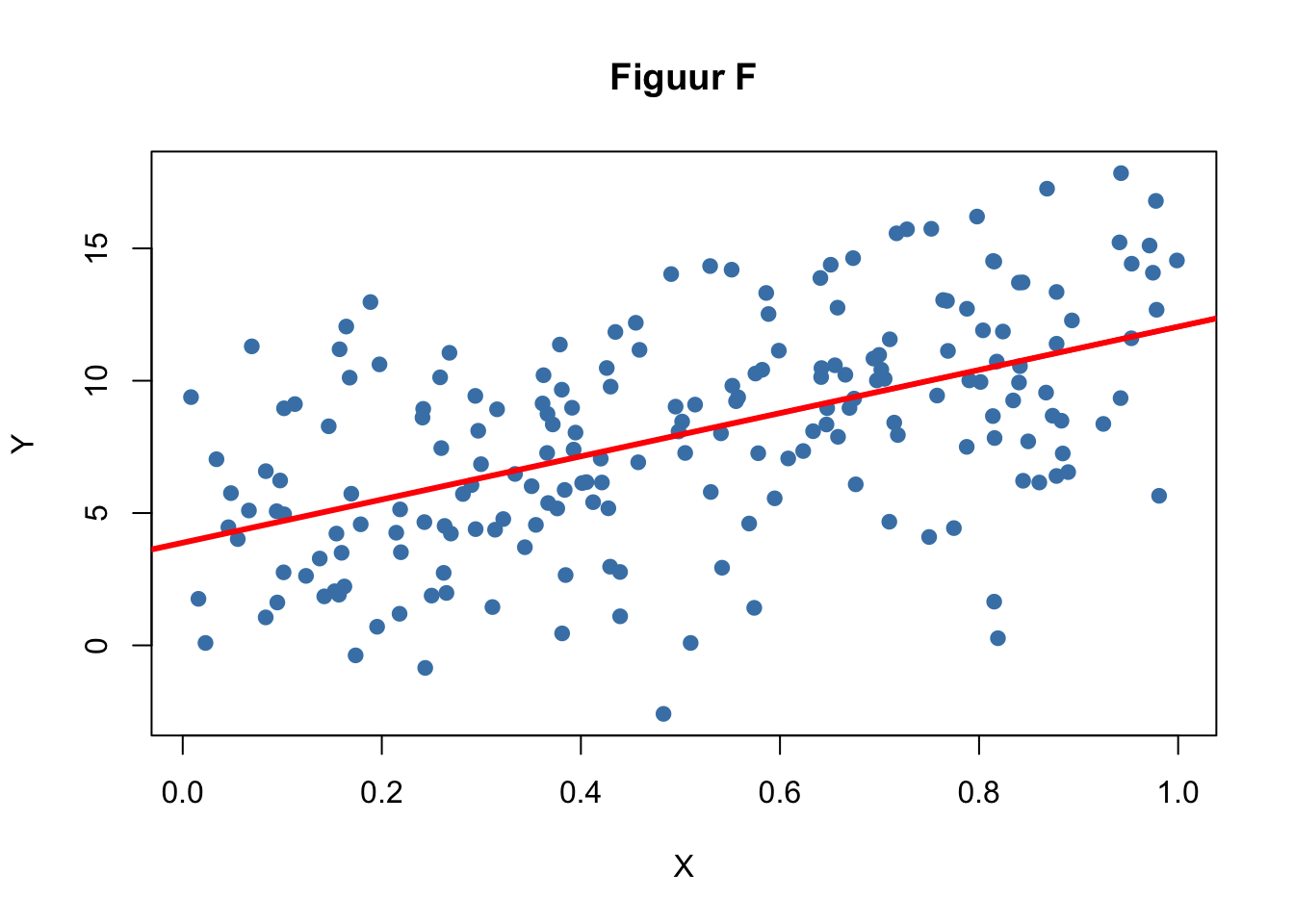
Stel dat dit data waren van 3 verschillende studies om het verband tussen X en Y te onderzoeken. Kun je dan redenen bedenken waarom deze resultaten zo verschillend zijn? Je mag hier zelf een onderzoek bedenken met een verklarende (X) en een uitkomstvariabele (Y).

Opgave 6

Voor deze opdracht zijn we geïnteresseerd in de associatie tussen de frequentie van hardlopen en de stress-levels van eerstejaars BMW studenten. Dit onderzoek loopt al een aantal jaren en ieder jaar worden opnieuw gegevens verzameld bij eerstejaars studenten. Tot 2018 werd een papieren vragenlijstje gebruikt. Hardloopfrequentie werd beantwoord op een schaal van 0 (= nooit) tot 7 (= dagelijks). De stress-levels van de studenten werden gemeten met een vragenlijst van 20 items, waarbij eindscore 0 = helemaal geen stress tot 20 = uitzonderlijk veel stress.

Op wat voor meetniveau worden deze twee variabelen gemeten?

Vanaf 2018 wordt een app gebruikt waar de deelnemer d.m.v. een schuifje aan te geven wat de hardloopfrequentie en het stressniveau is. Hardloopfrequentie is geschaald tussen 0 en 1, en stress is geschaald tussen 0 en 20 om zoveel mogelijk overeen te komen met het oorspronkelijke onderzoek. Iedere waarde tussen 0 en 20 is nu mogelijk.

Op wat voor meetniveau worden de variabelen nu gemeten?
Wat zijn voor- en nadelen van de nieuwe meetschaal?

Spreidingsdiagrammen zijn niet alleen handig voor het waarnemen van de sterkte van associatie tussen twee variabelen, ze zijn ook erg geschikt voor het detecteren van uitbijters. In de figuren hieronder zijn drie verschillende spreidingsdiagrammen weergegeven tussen de wekelijkse hardloopfrequentie en het stressniveau: figuur A representeert 2018, figuur B 2019 en figuur C 2020.

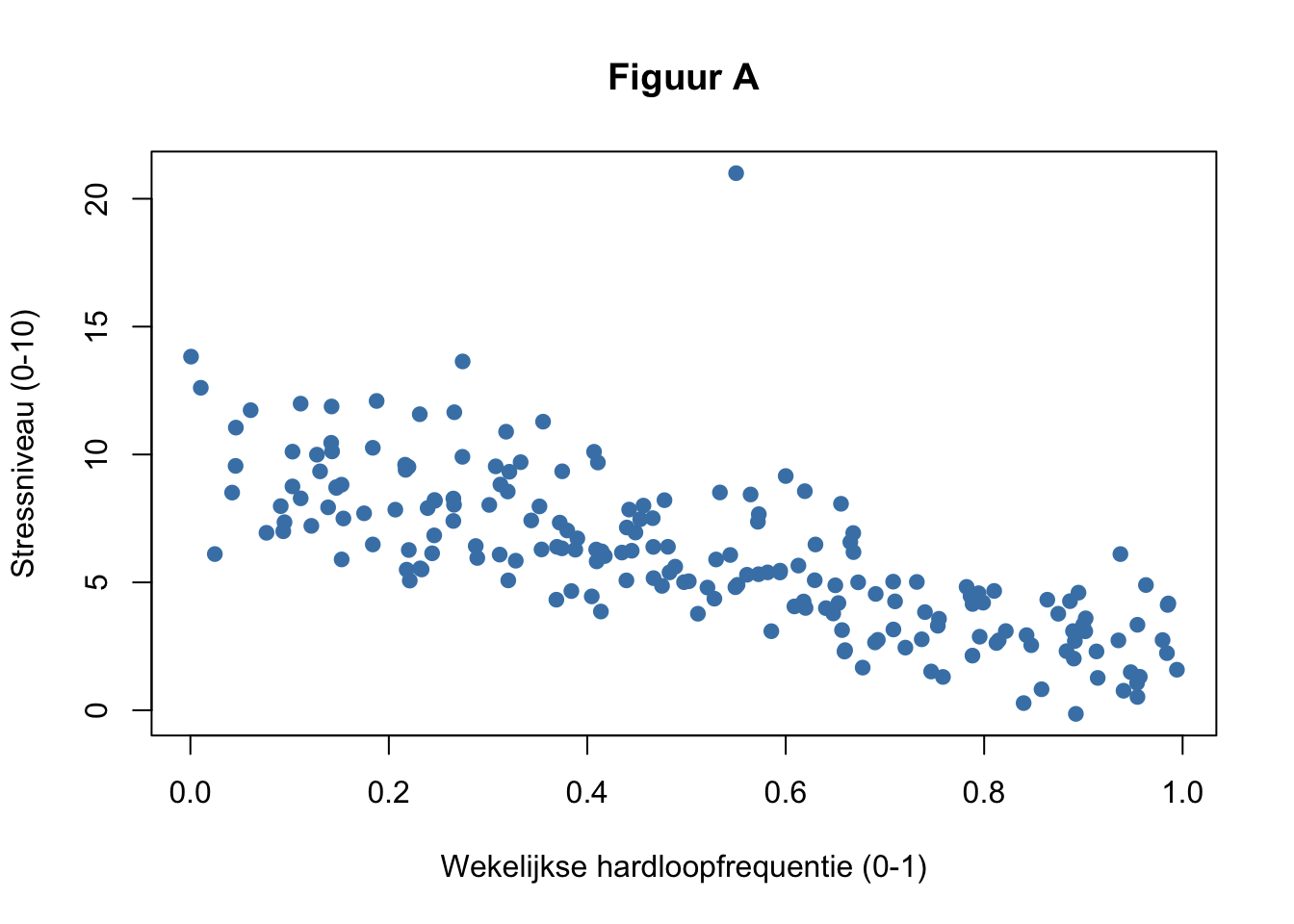
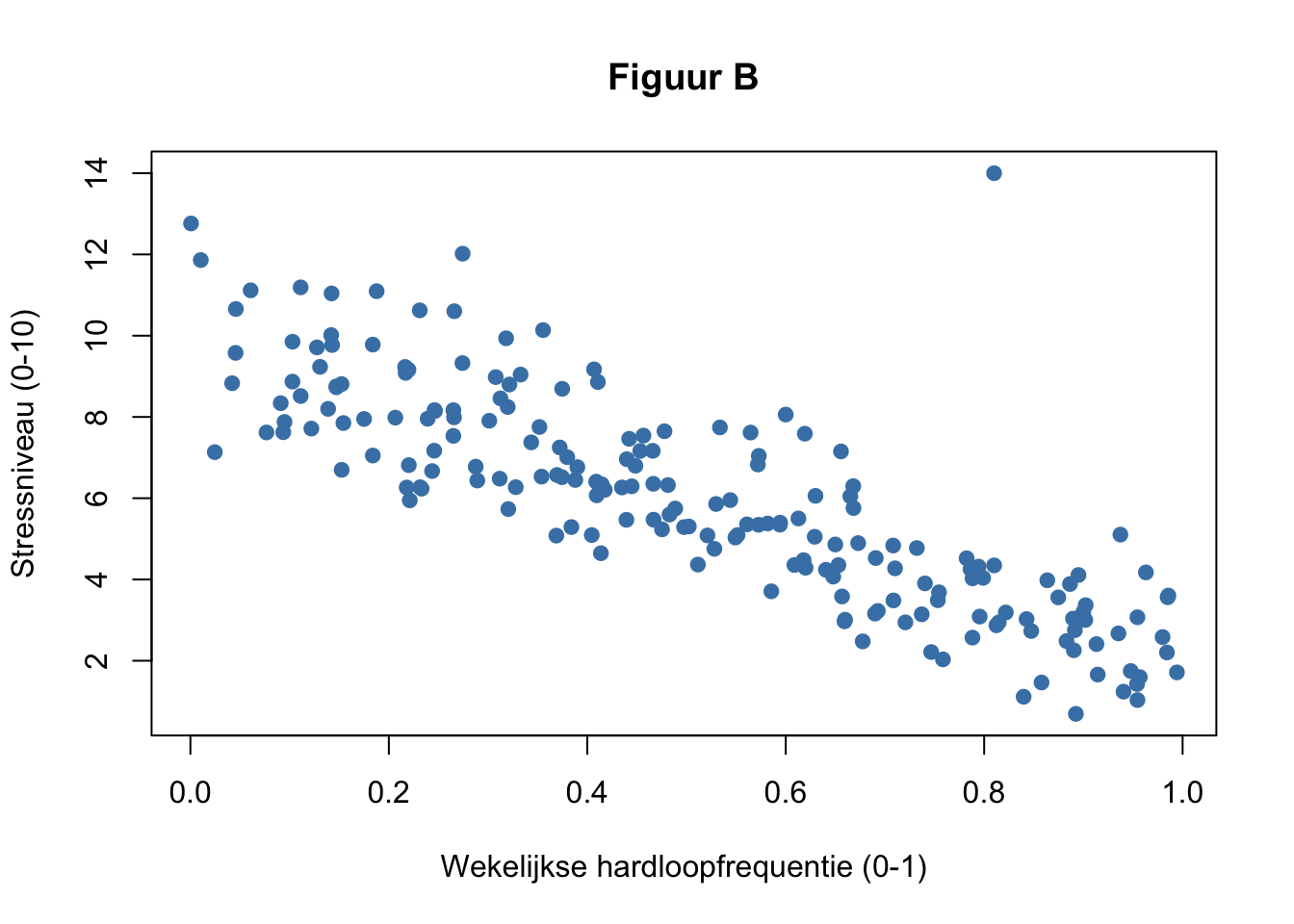
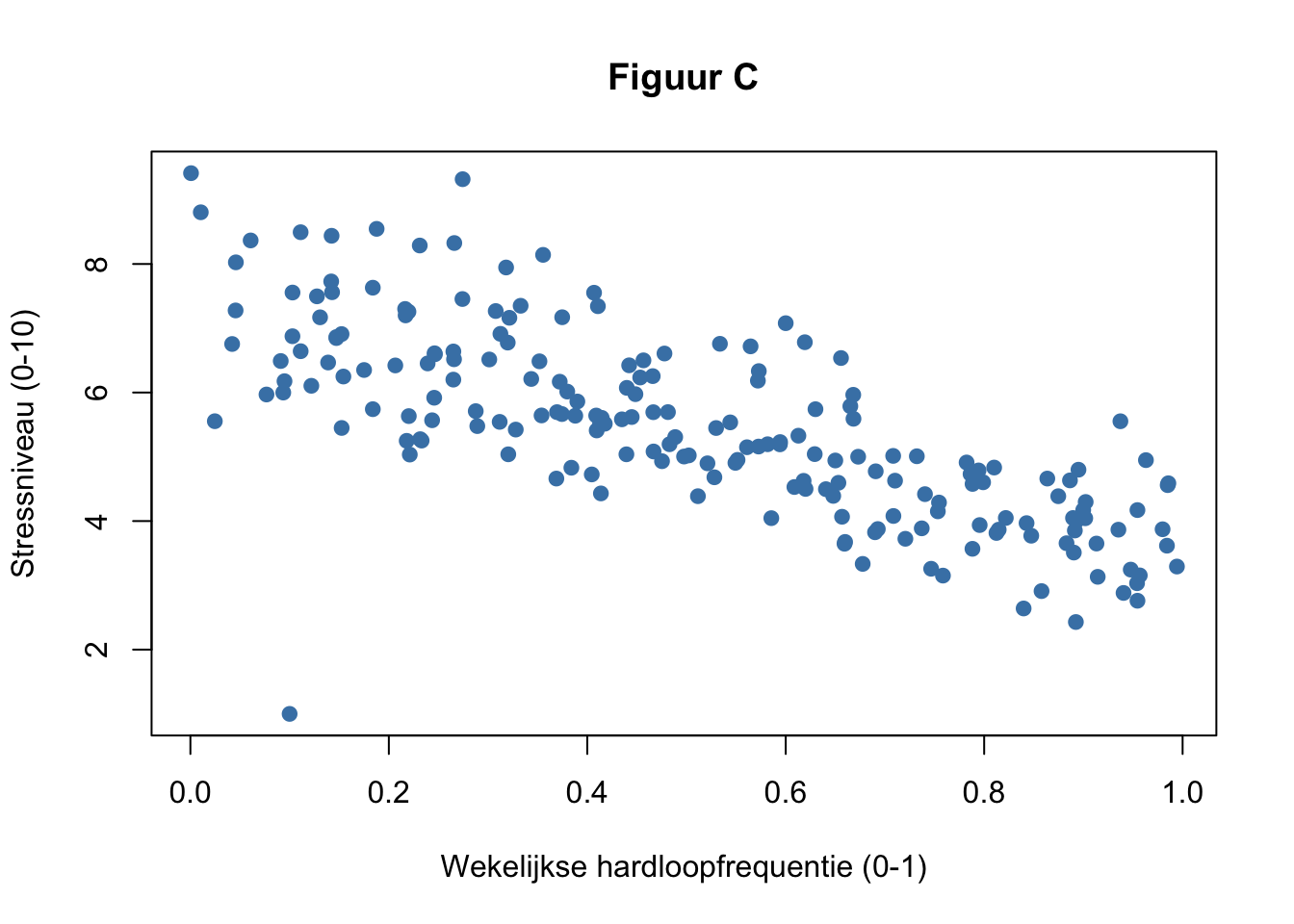
Welk van de uitbijters heeft het meeste invloed op de hellingshoek? Geef aan waarom.
Welk van de uitbijters heeft het meeste invloed op de correlatie tussen de variabelen? Geef aan waarom.
Welke uitbijter(s) zou je verwijderen? Beredeneer.

Opgave 7

Penicilline is een bioactieve stof die kan zorgen voor de remming van bacteriële groei. In een dosis-response studie werd bij verschillende concentraties penicilline (units/ml) gekeken naar de groeiremming van de bacterie.

Penicilline concentratie (units/ml)	Groeiremming
0.125	71.0
0.250	79.0
0.500	88.0
1.000	99.0
2.000	107.5
4.000	115.0
8.000	128.0
16.000	131.0

Kijk eens goed naar de waarden van deze reeks penicilline concentraties. Wat valt je op?

Hieruit zijn de volgende gegevens berekend: Gemiddelde en SD van de groeiremming: 102.3 en 22.1.

Penicilline	Ongetransformeerd	Log-2	Ln (=Log-e)	Log-10
Gemiddelde	3.98	0.50	0.35	0.15
SD	5.53	2.45	1.70	0.74
Corr met remming	0.825	0.997	0.997	0.997

De data kun je in spreidingsdiagrammen visualiseren:

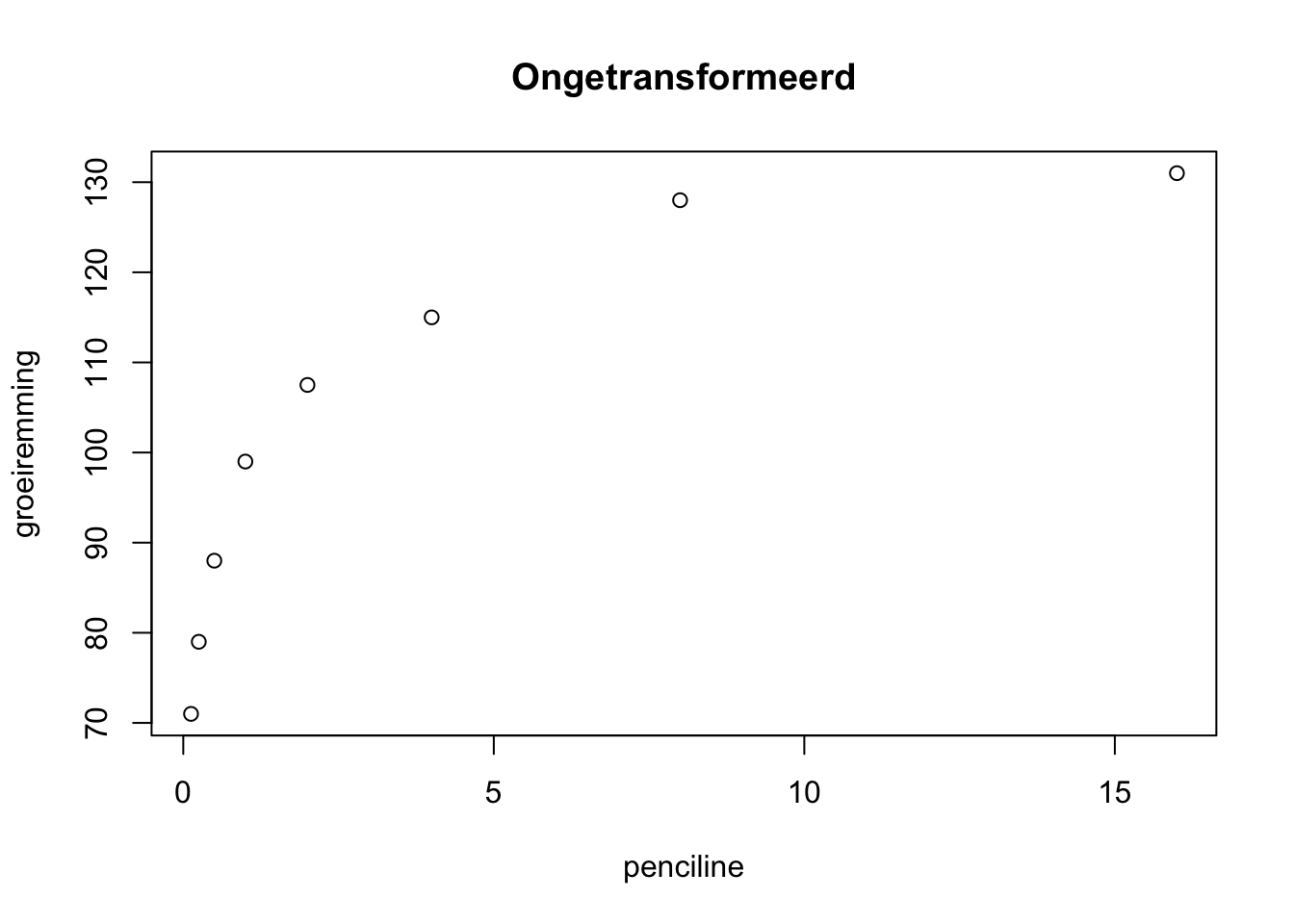
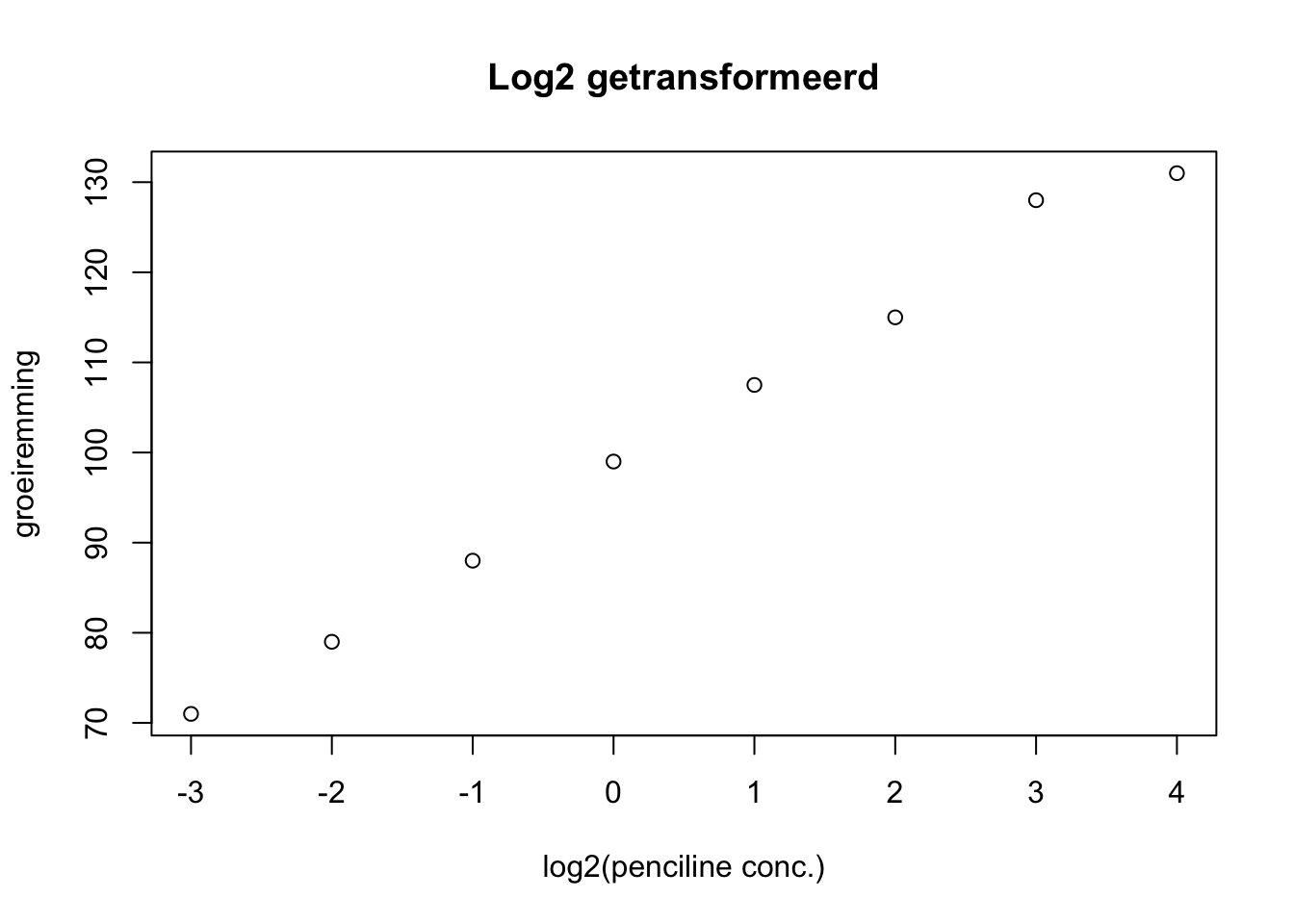
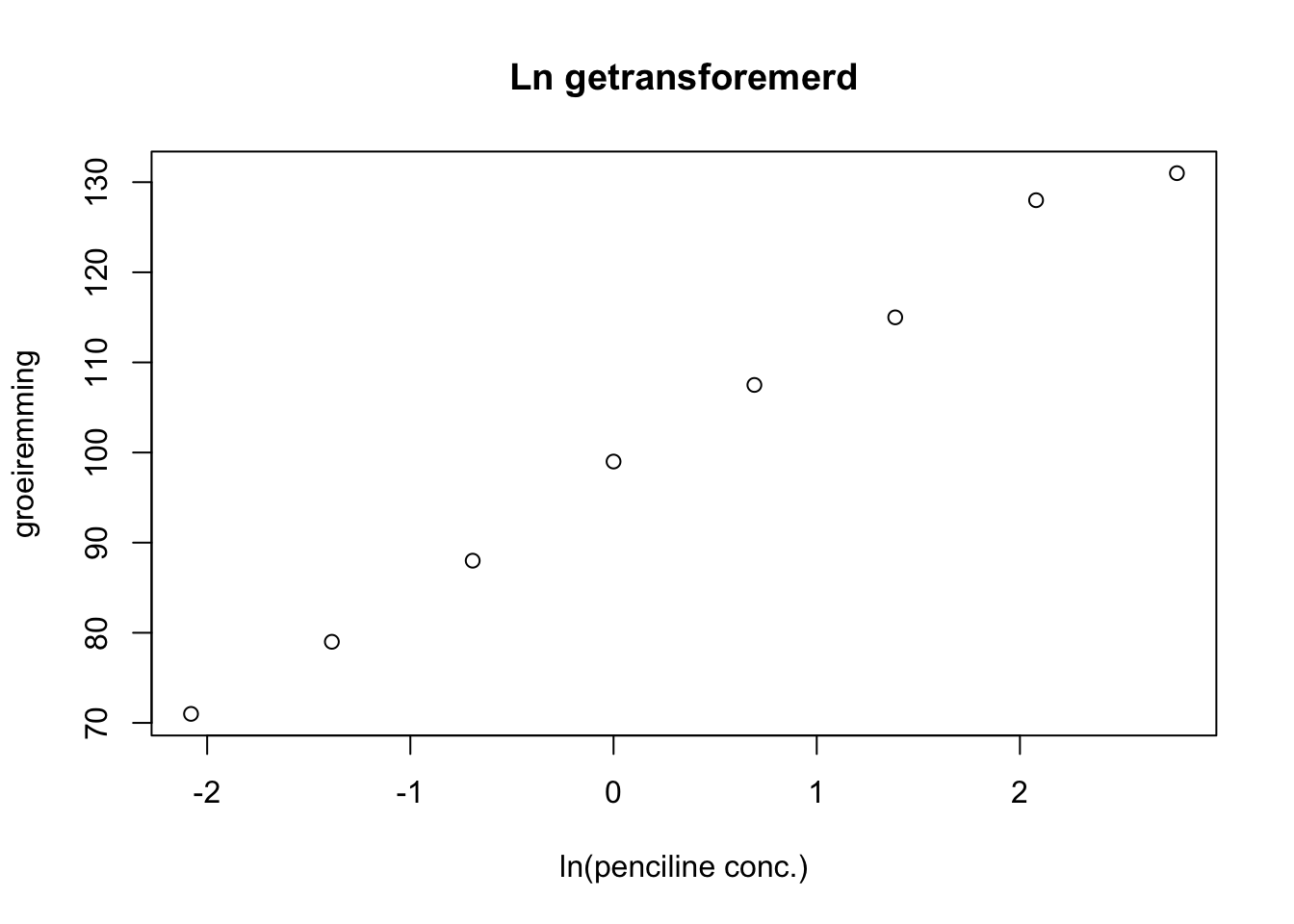
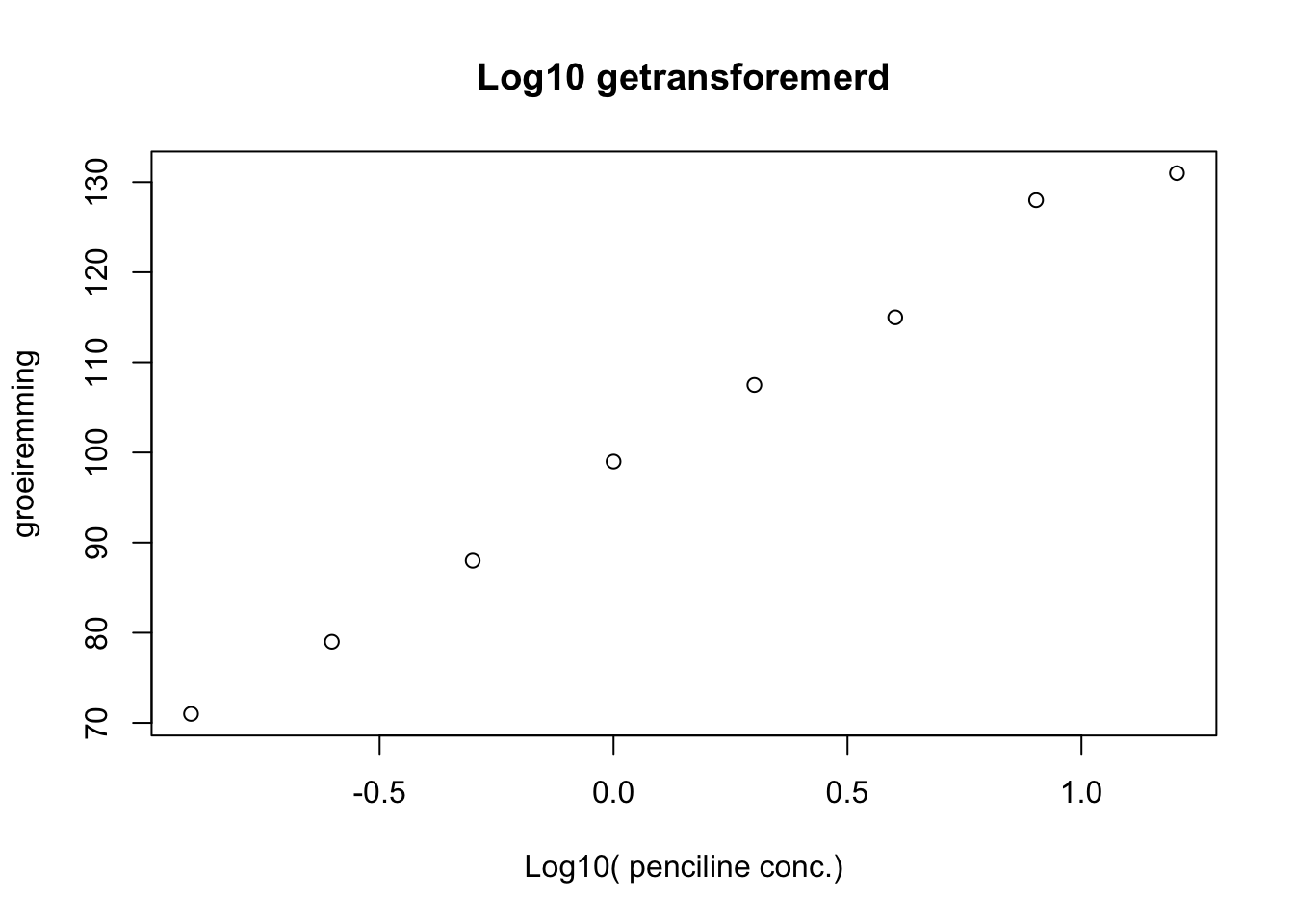
Stel de vergelijking op van de regressielijnen.
Bereken en interpreteer de proportie verklaarde varianties en verklaar waarom die in de vier analyses kunnen verschillen of juist overeen zullen komen.
Welke benadering heeft jouw voorkeur? Beargumenteer je antwoord met methodologische, statistische en medisch biologische redenen.
Voorspel de groeiremming bij een penicilline concentratie van 8 units/ml

Opgave 8

Inmiddels hebben we 2 leereenheden gehad waarin allerlei termen gebruikt zijn. Voordat we LE3 starten is het goed om na te gaan of je een goed begrip hebt van al deze termen. Zoek de betekenis op in het boek of in de zelfstudiedocumenten, en definieer in je eigen woorden (je kunt als je wilt ook de formule erbij schrijven). In de lijst staan een aantal synoniemen (soms ook de Engelse termen). Hier kun je naar dezelfde definitie verwijzen.

Asafsnijding:
Associatie:
Average:
Bias:
Correlatie:
Determinatiecoëfficiënt:
Gemiddelde:
Helling:
Intercept:
Interkwartielafstand:
Invloedrijke waarde:
Kwadratensom:
Kwartielen:
Mean:
Mediaan:
Nauwkeurigheid:
Populatie:
Precisie:
Q1 en Q3:
Q2:
Regressiecoëfficiënt:
Residuen:
SD:
Slope:
Standaardafwijking:
Standaarddeviatie:
Steekproef:
Sum of squares:
Uitbijter:
Variantie:
Variatie:
Zuiverheid:

De antwoorden zijn te vinden in het boek en de zelfstudies. Als je onzeker bent over een definitie, bespreek dit dan met je medestudenten, of vraag het een van de docenten.