Introductie

Maak opgaven 1-7 hieronder in je werkgroep. Je mag ook in je eentje werken, maar bij vragen en onduidelijkheden is het verstandig om eerst met je groep te overleggen. Je leert namelijk het meest door elkaar te bevragen en dingen aan elkaar uit te leggen. Opgaven 4-6 zijn groepsopdrachten. Probeer eerst zelf tot een oordeel te komen, maar overleg daarna met je groep, en probeer tot een gezamenlijk beoordeling te komen. Opgaven 8 en 9 zijn bedoeld als zelfstudie, en voorbereiding op de toets.

Opgave 1

Geef de meest toepasselijke nul- en alternatieve hypothesen voor de volgende experimenten. Bedenk daar zo nodig een uitkomstmaat, determinant en studieopzet bij.

  1. Een onderzoek of roken de oorzaak is van longkanker.

  2. Een onderzoek of de schade door planteneters aan een genetisch gemodificeerd gewas verschilt met die aan het niet-gemodificeerd gewas.

  3. Een onderzoek of het afval van een fabriek de vispopulatie beïnvloedt.

  4. Een onderzoek of het voorzien van veilige injectie plekken voor drugsverslaafden de HIV-transmissie beïnvloedt.

Opgave 2

Avandia is in gebruik als diabetes medicijn. Echter, Avandia is ook in verband gebracht met een verhoogd risico op hart- en vaatziekten. Een farmaceut heeft hiertoe onderzocht wat de potentiële impact is van het medicijn Avandia op de lipide waardes in het bloed van volwassen diabetes-patiënten. De gemiddelde baseline waarde van low-density lipoproteïne in een aselecte steekproef van 964 patiënten was milligram per deciliter (mg/dL). Het is bekend dat LDL-spiegels in de populatie volwassenen zo goed als normaal verdeeld zijn met een standaarddeviatie van σ = 30 mg/dL. Gegeven is een 95% betrouwbaarheidsinterval van het gemiddelde baseline LDL-level µ in de steekproef van dit onderzoek, onder de aanname dat σ van deze steekproef bekend is en hetzelfde als de σ in de populatie.

  1. Schrijf dit betrouwbaarheidsinterval uit naar een geschreven tekst in de context van de geschetste situatie.

  2. Volgens de Centers for Disease Control and Prevention (het Amerikaanse RIVM) is de gemiddelde LDL-spiegel voor gezonde volwassenen 191 mg/dL. Gebruik de z-toets met een onzekerheid van 5% om te testen of de gemiddelde LDL-spiegel onder suikerziektepatiënten verschilt van die van gezonde Amerikanen. Gebruik het 4-stappen plan.

  3. Was het nodig in dit geval om een formele toets te gebruiken voor deze vraag? Verklaar je antwoord.

  4. Een van de “simpele voorwaarden” voor inferentie van een populatie gemiddelde is dat de standaarddeviatie van de populatie σ bekend is. Leg uit waarom deze aan deze aanname mogelijk niet voldaan wordt in dit onderzoek.

Opgave 3

Het Amerikaans Institute of Medicine heeft bepaald dat de aanbevolen dagelijkse hoeveelheid (ADH) van zoutinname voor volwassenen en tieners 2300 milligram (mg) per dag is. Onderzoekers denken dat door hun voedingspatroon tieners meer zout innemen dan aanbevolen. In een aselecte steekproef van 3727 tieners in de V.S. vond men een gemiddelde zoutinname van 3486 mg per dag. We nemen aan dat de standaarddeviatie van zoutinname in deze populatie 800 mg/dag is.

  1. Betekent dit dat de tieners in de V.S. meer dan de hoogst toelaatbare waarde van zout innemen per dag?

  2. Wat zijn de H0 en H1 als je deze vraag zou willen beantwoorden met een statistische toets? Geef duidelijk aan wat de waarde van µ is in deze hypothese.

  3. Gebruik het 4-stappen plan om de toets uit te voeren en antwoord te krijgen op de vraag.

Opgave 4

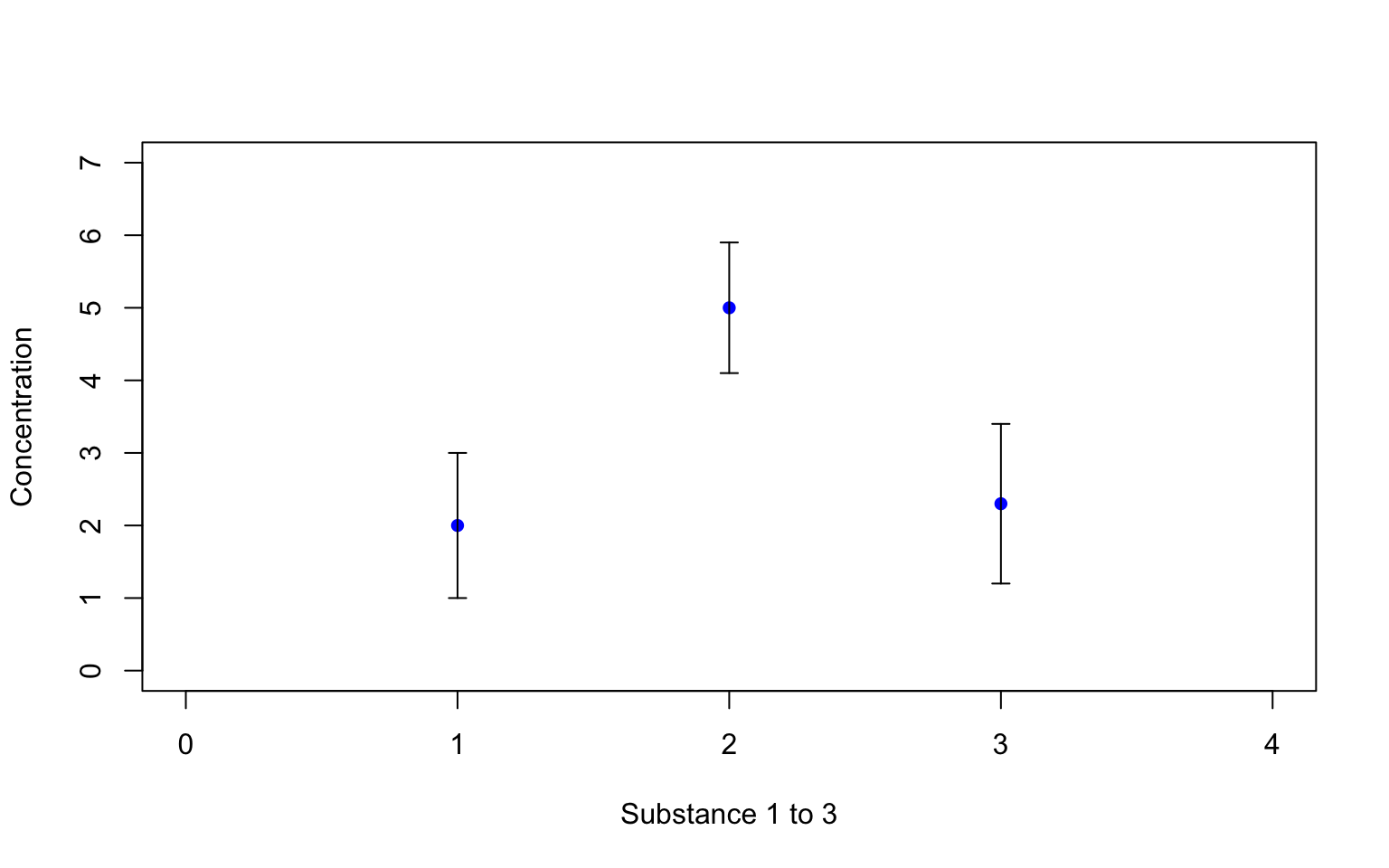
Het figuur is overgenomen van een website van de U.S. National Enviromental Laboratory. In deze figuur staan van een steekproef (monsters) de gemiddelde concentraties van 3 radioactieve substanties met een 95% betrouwbaarheidsinterval weergegeven. Als tekst bij de figuur staat: “the first plotted mean is 2.0 ± 1.1, so there is a 95% chance that the actual result is between 0.9 and 3.1, a 2.5% chance that it is less than 0.9 and 2.5% chance that it is greater than 3.1.” Is dit een juiste interpretatie van een betrouwbaarheidsinterval? Beargumenteer je antwoord.

Opgave 5

  1. Statistische significantie wordt vaak gerapporteerd in wetenschappelijk onderzoek. Gevraagd wat het betekent, vertelt een student: ‘als een resultaat statistisch significant is, wil dat zeggen dat het resultaat niet alleen door steekproefvariabiliteit verklaard kan worden als de nulhypothese waar is.’ Denk je dat dit statement correct is? Beargumenteer je antwoord.

  2. Gevraagd wat de betekenis van ‘de p-waarde was 0,07’ is, beantwoordt een student: ’Dat betekent dat er een kans van 0,07 is dat de nulhypothese waar is.’ Denk je dat deze uitleg correct is? Beargumenteer je antwoord.

Opgave 6

Schets een standaard normaalverdeling voor de Z toetsingsgrootheid (‘test statistic’). Geef hierbij aan voor welke waarden van Z, de toets significant is voor α = 1% in een éénzijdige toets en voor α = 5% in een éénzijdige toets. Leg uit waarom een toets die significant is op het 1% niveau, ook significant is voor een toets op het 5% niveau. Geldt dit ook andersom, dus voor een toets die met α = 5% significant is, is die dan ook significant bij α = 1%?

Opgave 7

Een neurologisch onderzoeker test het effect van een medicijn op de responstijd van muizen in een taak. De gemiddelde responstijd voor muizen die geen medicijn krijgen bedraagt 1.5 seconden. De onderzoeker wil toetsen of de gemiddelde responstijd bij het gebruik van medicijnen verandert. Stel je voor dat in werkelijkheid het populatie gemiddelde van de responstijd van muizen die dit medicijn gebruiken 1.8 seconden is en het onderscheidende vermogen (de statistische power) van de toets is 90%, dan a. is de kans om H0 te verwerpen 10% b. is de kans om H0 niet te verwerpen 10% c. is de kans om H0 niet te verwerpen 90%

Tip: maak voor het beantwoorden van deze vraag een 2x2 tabel met in kolommen de werkelijkheid (1.5 sec, net als onder H0 of 1.8 sec, zoals in deze opgave) en in rijen de uitslag van de toets (H0 handhaven of H0 verwerpen). In welke cellen staan dan de statistische power, de type I fout en de type II fout?

Opgave 8

(zelfstudie/tentamenvoorbereiding) Maak uit hoofdstuk 16 (een samenvatting van heel deel II van het boek) opgave 16.17. Bespreek dit met je groep en met de docent van het werkcollege. Het antwoord staat achter in het boek.

Opgave 9

(zelfstudie/tentamenvoorbereiding) In LE2 werd je gevraagd een aantal statistische begrippen te beschrijven. Breid de tabel uit met termen die we in de laatste drie leereenheden hebben gebruikt, zie de volgende bladzijde. Zoek de betekenis op in het boek of in de zelfstudiedocumenten, en definieer ze in je eigen woorden (je kunt als je wilt ook de formule erbij schrijven). In de lijst staat een aantal synoniemen (soms ook de Engelse termen). Hier kun je naar dezelfde definitie verwijzen.

  • α
  • Alternatieve hypothese
  • Aselecte steekproef
  • Betrouwbaarheidsinterval
  • Centrale limietstelling
  • Confidence interval
  • Eénzijdige toets
  • Estimate
  • Foutmarge
  • Margin of error
  • Normale verdeling
  • Nulhypothese
  • p-waarde
  • Q-Q plot
  • Representatieve steekproef
  • Scatter plot
  • Significantieniveau
  • Standaard normale verdeling
  • Standaardfout van het gemiddelde
  • Statistisch significant
  • Steekproefvariabiliteit
  • Steekproefverdeling
  • Toetsingsgrootheid
  • Tweezijdige toets
  • Type I fout
  • Vier-stappen plan
  • z-score
  • z-toets
  • z-verdeling