Introductie

Maak de opgaven hieronder in je werkgroep. Je mag ook in je eentje werken, maar bij vragen en onduidelijkheden is het verstandig om eerst met je groep te overleggen. Je leert namelijk het meest door elkaar te bevragen en dingen aan elkaar uit te leggen. Opgaven 3-6 zijn discussieopdrachten. Probeer eerst zelf tot een oordeel te komen, maar overleg daarna met je groep, en probeer tot een gezamenlijk antwoord te komen.

Opgave 1

Stel dat een populatieverdeling niet symmetrisch is, maar rechts-scheef, d.w.z. de scores liggen niet mooi rond het gemiddelde maar de rechterstaart is breder zoals in onderstaand histogram.

  1. Hoe ziet dan de verdeling van steekproefgemiddelden van steekproeven met grootte 50 eruit? (Wat is de vorm van de verdeling)?

  2. Wat is de standaarddeviatie van de verdeling van steekproefgemiddelden met grootte 50? Vergelijk dit met de standaarddeviatie in de populatie. Let op: je hoeft hier niet een waarde uit te rekenen, we vragen hier hoe je deze waarde zou uitrekenen.

Opgave 2

De arts van Anna maakt zich zorgen dat ze mogelijk zwangerschapsdiabetes (hoge glucosespiegels tijdens de zwangerschap) heeft. De diagnose zwangerschapsdiabetes wordt gesteld als de glucosespiegel een uur na consumptie van een suikerhoudende drank hoger is dan 140 milligram per deciliter (mg/dl). Maar er is altijd variatie in het werkelijke glucosegehalte, ook binnen personen. Dat betekent dat Anna’s gemeten glucosespiegel een uur na het drinken van de suikerhoudende drank kan variëren. Neem aan dat de glucosespiegel van Anna verdeeld is volgens de normale verdeling met µ = 125 mg/dl en σ = 10 mg/dl.

  1. Als er een enkele glucosemeting wordt gedaan, wat is dan de kans dat Anna de diagnose zwangerschapsdiabetes krijgt?

  2. Als er op 4 afzonderlijke dagen wordt gemeten en het gemiddelde resultaat wordt vergeleken met het criterium 140 mg/dl, wat is dan de kans dat Anna de diagnose zwangerschapsdiabetes krijgt?

Opgave 3

Zijn de volgende uitspraken JUIST of ONJUIST? Bespreek je antwoorden met je groep.

  1. Hoe groter de steekproef, des te betrouwbaarder de schatting van het populatiegemiddelde.

  2. Wanneer er in de populatie heel weinig variatie is, dan hebben we aan een relatief kleine steekproef genoeg om een betrouwbare schatting van het populatiegemiddelde te kunnen maken.

Opgave 4

  1. Stel dat we het aantal waarnemingen in een steekproef verdubbelen. Wat gebeurt er dan met de standaardfout van het gemiddelde?

  2. Wat betekent een verkleining van de standaardfout voor de betrouwbaarheid van het steekproefgemiddelde als schatting voor het populatiegemiddelde?

Opgave 5

De verdeling van het alcoholgehalte in het bloed van bestuurders in de avond is erg scheef. De meeste bestuurders rijden niet onder de invloed van alcohol, en sommige beperken hun alcoholgebruik, terwijl enkele bestuurders dronken zijn. Als je berekeningen volgens de normale verdeling wilt maken, en je gebruikt de steekproefverdeling van het gemiddelde alcoholpercentage in het bloed van bestuurders in de avond, zou een aselecte steekproef van 10 bestuurders dan voldoende zijn? 50 bestuurders? 200 bestuurders? Leg je antwoorden uit aan je groep en schrijf het daarna op.

Opgave 6

Lees de volgende twee krantenberichten van de Volkskrant (boven: VK 11/4/2021; onder: VK 24/4/2021) door en kijk naar de figuren. Het eerste bericht gaat over het aantal ziekenhuisopnamen, het tweede over het aantal besmettingen.

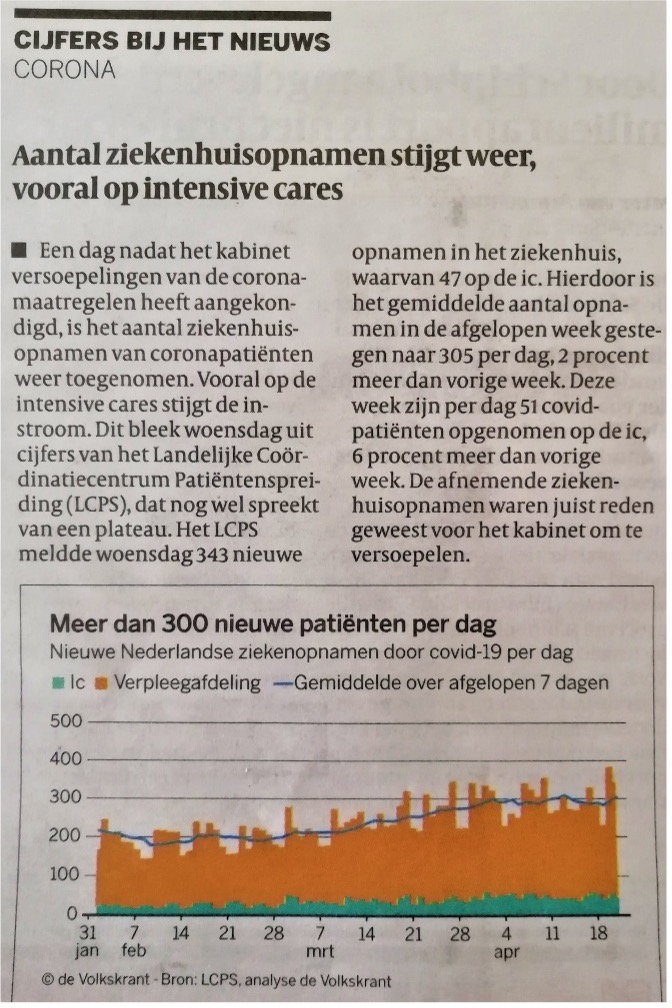
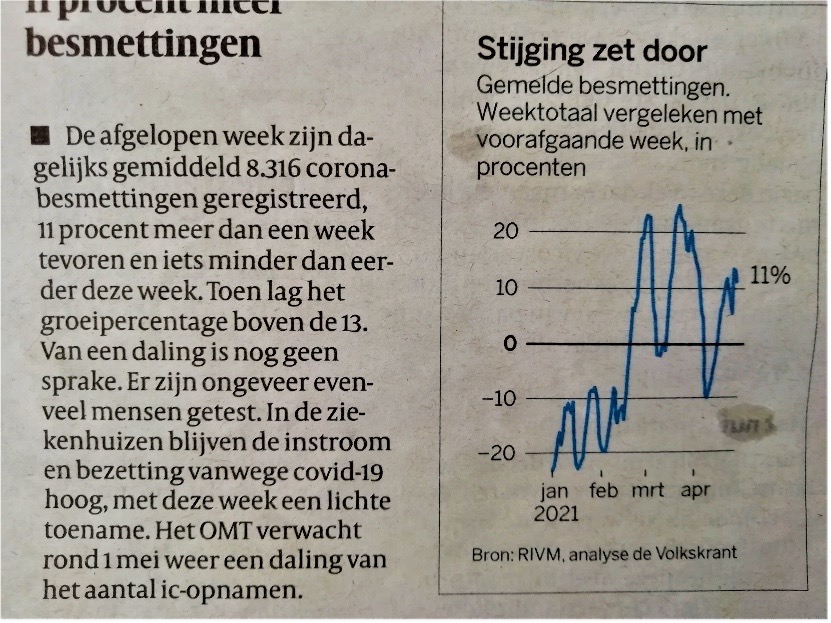
  1. Coronacijfers worden op verschillende manieren gerapporteerd. Sommige bronnen kijken bijvoorbeeld elke dag naar het aantal besmettingen (‘vandaag is het boven de 8000, 100 meer dan gisteren!’), maar andere bronnen zoals de Volkskrant kijken naar het 7-daagse gemiddelde. Waarom zou de Volkskrant voor dat laatste kiezen?

  2. Zijn de verschillen in gerapporteerde coronacijfers door verschillende bronnen een goed voorbeeld van steekproefvariabiliteit? Waarom wel/niet?

  3. Hoeveel besmettingen zijn er per dag volgens de Volkskrant? Is dit aantal het resultaat van een steekproef of is het een schatting?

  4. Waarom kijken sommige bronnen alleen naar ziekenhuis of IC opnamen, terwijl andere kijken naar het aantal geregistreerde besmettingen? Welke van deze maten is volgens jou beter om te rapporteren? Verklaar je antwoord.

Opgave 7

In de 2012 ronde van het National Health and Nutrition Examination Survey (NHANES), een studie met meer dan 20.000 deelnemers, werd een gemiddelde tailleomvang van volwassen vrouwen in de VS van 100,9 gerapporteerd, met een 95% betrouwbaarheidsinterval van 99,8 tot 102,0.

Je vraagt aan je vrienden om uit te leggen wat dit resultaat betekent.

  1. Een vriend gelooft dat dit betekent dat 95% van alle volwassen vrouwen in de VS een tailleomvang tussen 99,8 en 102,0 heeft. Is dit juist? Onderbouw je antwoord.

  2. Een andere vriend is het daar niet mee eens. Hij gelooft dat we 95% zekerheid hebben dat de ware gemiddelde tailleomvang van volwassen vrouwen 100,9 cm is. Is dit juist? Onderbouw je antwoord.

Opgave 8

De Associated Press heeft een uitleg van hun betrouwbaarheidsinterval geplaatst aangaande een van hun opiniepeilingen. Leg kort maar duidelijk uit wat hier incorrect aan is. “For a poll of 1600 adults, the variation due to sampling error is no more than three percentage points either way. The error margin is said to be valid at the 95 percent confidence level; this means that, if the same questions were repeated in 20 polls, the result of at least 19 surveys would be within three percentage points of the result of this survey.”

Opgave 9

Opgave 7 geeft een 95% betrouwbaarheidsinterval voor het gemiddelde tailleomvang van volwassen vrouwen in de VS volgens het NHANES 2012: [99,8 - 102,0].

  1. Schrijf dit betrouwbaarheidsinterval uit naar een geschreven tekst in de context van de geschetste situatie.

  2. Herschrijf dit interval naar een format waarin de “margin of error” (foutmarge) zichtbaar is, ook wel “schatter ± foutmarge”.

  3. Wat zou er veranderen aan het betrouwbaarheidsinterval als deze 90% in plaats van 95% zou zijn? Leg dit uit.

Opgave 10

Opgave 7 geeft een 95% betrouwbaarheidsinterval voor de gemiddelde tailleomvang van volwassen vrouwen in de VS volgens het NHANES 2012: [99,8 - 102,0].

  1. Welke kritieke waarde werd gebruikt om dit 95% betrouwbaarheidsinterval te berekenen?

  2. Wat is de standaarddeviatie van de steekproefverdeling van de gemiddelde tailleomvang x̅?

  3. Laat de berekeningen zien die nodig zijn om tot de uitkomst van 95% betrouwbaarheidsinterval te komen.