COO4: Descriptive Statistics in R

In this computer lab, you will learn how to describe a sample using simple plots and descriptive statistics. We concentrate here on continuous (or “numeric”) outcome variables, looking at one group, two or more groups, and the relationship between a continuous outcome variable and a continuous explanatory variable (determinant).
In a later COO you will learn how to describe a categorical variable, and associations between two categorical variables.

Preparation
Descriptive statistics, continuous outcome (step-by-step)

1.1 Describing 1 group
1.2 Describing > 1 group
1.3 Aside: transformations
1.4 relationship to 1 continuous explanatory variable

Practice what you’ve learned

You are asked to answer a number of questions (in bold and numbered throughout).

0. Preparation

Before starting, please download the file BMISBP.csv and save it locally.

We will start the R session by installing (if necessary) and loading the packages we need for the exercises below. We will be using datasets and/or functions from the NHANES package and the psych package. If you are using these packages for the first time, you will first need to install them. Do this either via the RStudio menu (Tools-Install Packages), or with these commands:

install.packages("NHANES") # put the package name between quotation marks
install.packages("psych")
install.packages("car")

You only need to install a package once. At the beginning of every R/Rstudio session, you need to load the packages you will be using:

library(NHANES)
library(psych)
library(car)

For the following exercises, we will use two datasets:

BMISBP.csv, a comma-separated dataset (which you have already downloaded), and
NHANES, a dataset built into the NHANES package

1. Descriptive statistics for a continuous outcome, step by step

We will start by looking at systolic blood pressure of adults in the NHANES sample. This dataset is a subset of the National Health and Nutrition Examination Survey (NHANES). First we load the data frame and get some information about it:

data(NHANES)
?NHANES

Question 1. What type of study design is this?

We’ll use the function dim() (dimensions) to see how many people are in the dataset provided (number of rows), and how many variables (number of columns).

dim(NHANES)

## [1] 10000    76

The dataset contains 76 columns, or variables, from 10000 participants, in the rows.

It can also be useful to look at the names of the variables (columns) in your data frame:

colnames(NHANES)

##  [1] "ID"               "SurveyYr"         "Gender"           "Age"              "AgeDecade"       
##  [6] "AgeMonths"        "Race1"            "Race3"            "Education"        "MaritalStatus"   
## [11] "HHIncome"         "HHIncomeMid"      "Poverty"          "HomeRooms"        "HomeOwn"         
## [16] "Work"             "Weight"           "Length"           "HeadCirc"         "Height"          
## [21] "BMI"              "BMICatUnder20yrs" "BMI_WHO"          "Pulse"            "BPSysAve"        
## [26] "BPDiaAve"         "BPSys1"           "BPDia1"           "BPSys2"           "BPDia2"          
## [31] "BPSys3"           "BPDia3"           "Testosterone"     "DirectChol"       "TotChol"         
## [36] "UrineVol1"        "UrineFlow1"       "UrineVol2"        "UrineFlow2"       "Diabetes"        
## [41] "DiabetesAge"      "HealthGen"        "DaysPhysHlthBad"  "DaysMentHlthBad"  "LittleInterest"  
## [46] "Depressed"        "nPregnancies"     "nBabies"          "Age1stBaby"       "SleepHrsNight"   
## [51] "SleepTrouble"     "PhysActive"       "PhysActiveDays"   "TVHrsDay"         "CompHrsDay"      
## [56] "TVHrsDayChild"    "CompHrsDayChild"  "Alcohol12PlusYr"  "AlcoholDay"       "AlcoholYear"     
## [61] "SmokeNow"         "Smoke100"         "Smoke100n"        "SmokeAge"         "Marijuana"       
## [66] "AgeFirstMarij"    "RegularMarij"     "AgeRegMarij"      "HardDrugs"        "SexEver"         
## [71] "SexAge"           "SexNumPartnLife"  "SexNumPartYear"   "SameSex"          "SexOrientation"  
## [76] "PregnantNow"

To keep things simple for the following exercises, we will concentrate on only the second survey (2011-2012), and use only the adults in the sample. Make a new dataframe d, containing this selection, and check how many participants are left:

d <- data.frame(NHANES[NHANES$SurveyYr == "2011_12" & NHANES$Age >= 18,])
dim(d)

## [1] 3707   76

So we continue with the 3707 adult participants. Note that we still have 76 variables.

In COO2 you learned the function View() to examine an entire data frame. With such a large data frame, it can be useful to just look at the first few lines of data frame with which you are working, to get a sense of the structure. You can do this with the head() function. Use:

head(d)

By default, head() displays the first 6 rows of data; you can change the number of rows displayed using the option n=. Try:

head(d, n = 10)

1.1 Describing 1 group

Make a histogram and boxplot of systolic blood pressure (SBP):

hist(d$BPSysAve, main = "Systolic Blood Pressure US Adults",
        xlab = "Systolic Blood Pressure (mmHg)")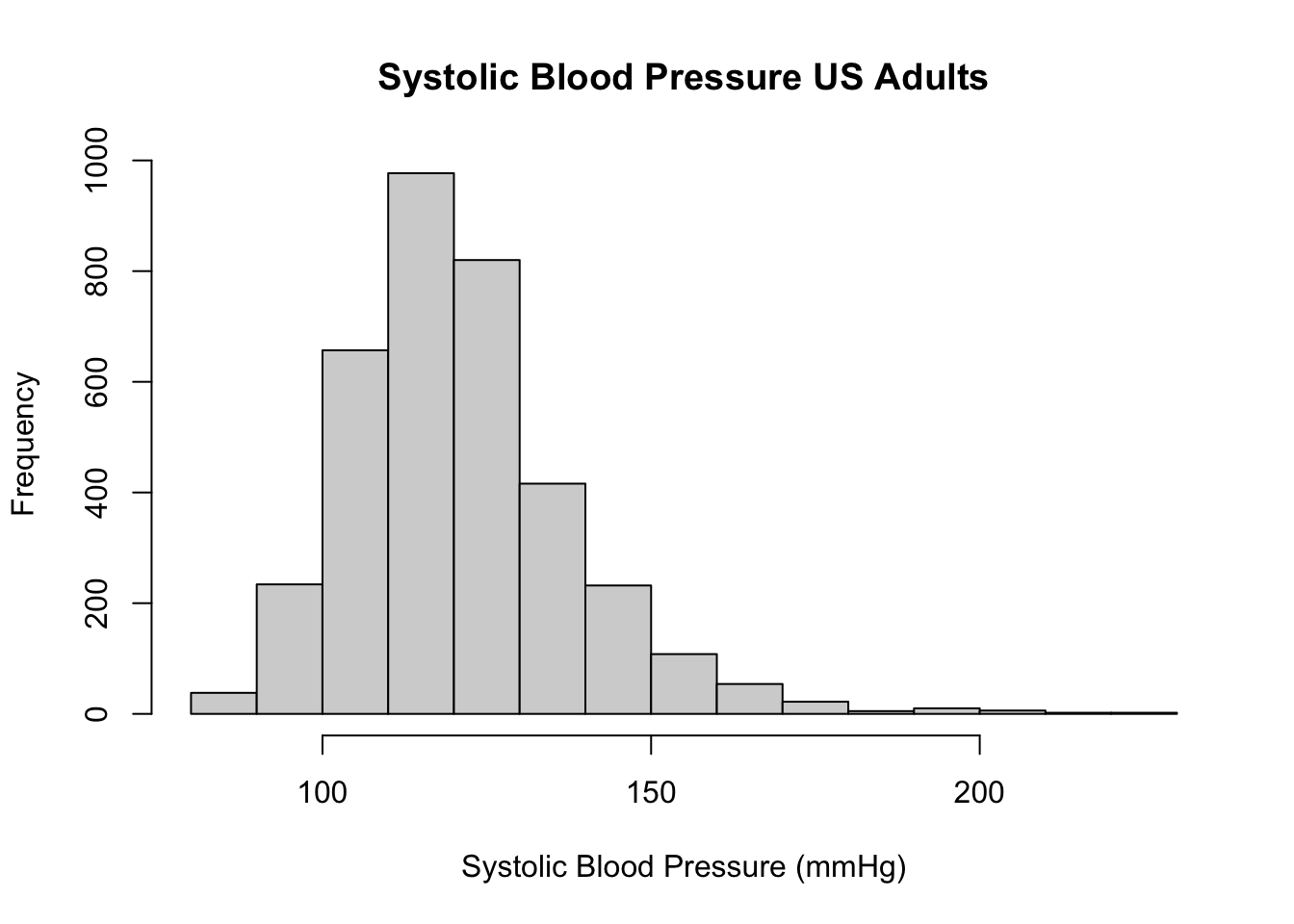

boxplot(d$BPSysAve, main = "Systolic Blood Pressure US Adults",
        ylab = "Systolic Blood Pressure (mmHg)")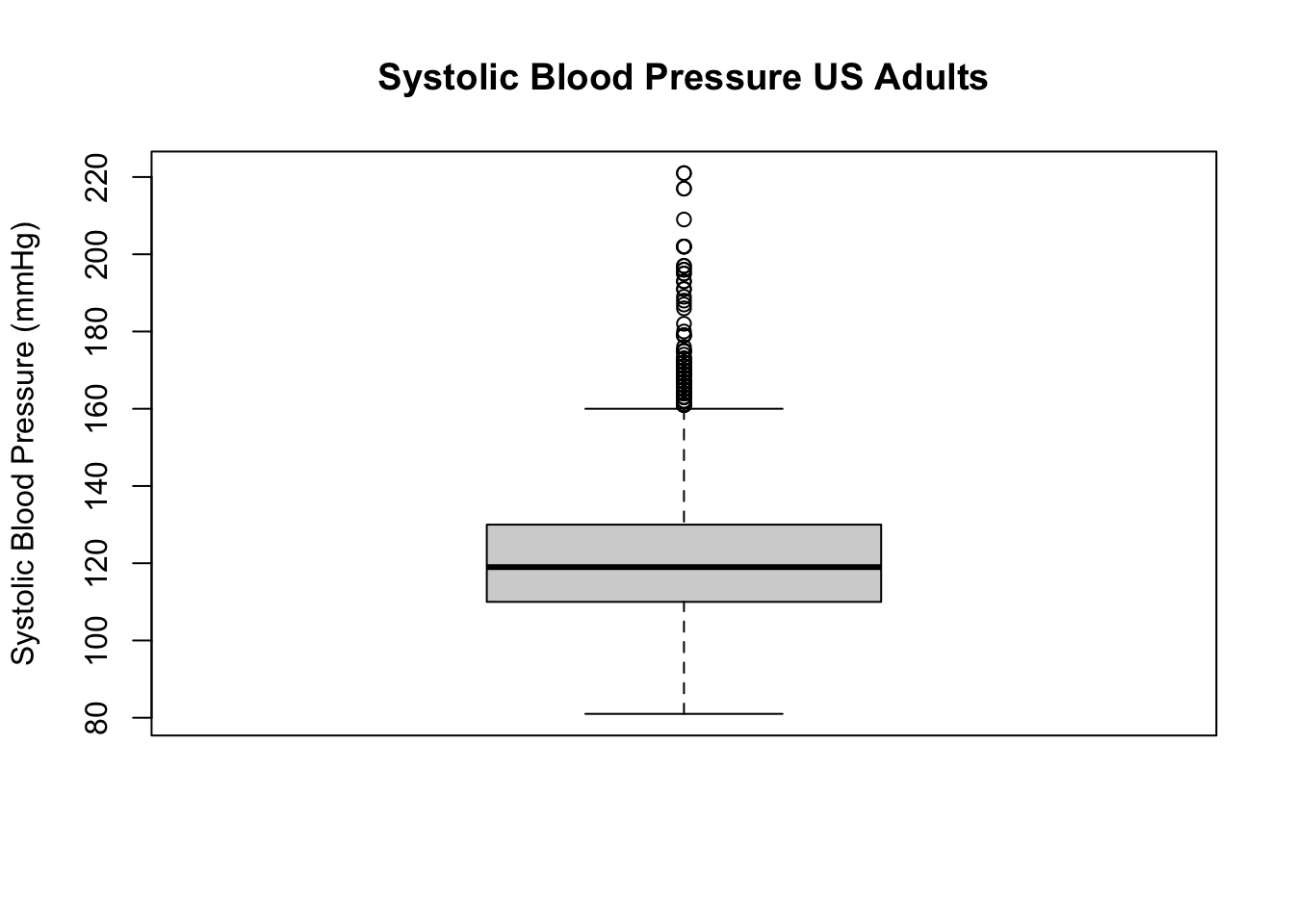

Question 2. Describe the shape of the distribution of SBP. Which descriptive statistics would you prefer for the location and variation (spread)?

Before continuing, see if you can read off the median SBP in the sample. What are the first and third quartiles, and what is the interquartile range? Can you guess (approximately) what the mean will be? And the standard deviation?

Question 2a. Write down your estimates for the sample quartiles, IQR, mean and SD.

Now we’ll check these estimates. You’ve seen several of the functions (mean, median, sd) earlier. IQR() is the interquartile range.

median(d$BPSysAve, na.rm = TRUE)

## [1] 119

mean(d$BPSysAve, na.rm = TRUE)

## [1] 121.458

quantile(d$BPSysAve, probs = c(0.25, 0.75), na.rm = TRUE)

## 25% 75% 
## 110 130

IQR(d$BPSysAve, na.rm = TRUE)

## [1] 20

sd(d$BPSysAve, na.rm = TRUE)

## [1] 17.1919

Do you understand the quantile function? If not, try ?quantile.

Question 2b. How do your guesses compare to the estimates given by R? If your guess was far off (say, more than 5 mmHg), why was that?

Getting all those statistics took a lot of lines of code. Fortunately, someone wrote a nice function to get all the important descriptive statistics for a variable, either for everyone in the dataset, or stratified (split up) by a factor (grouping) variable. The function we want is describe, from the psych package. Note that we use the skew=FALSE option to repress some of the default output, and the quant and IQR options to get some output we do want.

describe(d$BPSysAve, na.rm = TRUE, skew = FALSE, quant = c(0.25, 0.5, 0.75), IQR = TRUE)

##    vars    n   mean    sd median min max range   se IQR Q0.25 Q0.5 Q0.75
## X1    1 3583 121.46 17.19    119  81 221   140 0.29  20   110  119   130

Let’s now take a look at the distribution of testosterone in the sample.

hist(d$Testosterone, main = "Testosterone Level US Adults",
        xlab = "Testosterone (ng/dL)")
boxplot(d$Testosterone, main = "Testosterone Level US Adults",
        ylab = "Testosterone (ng/dL)")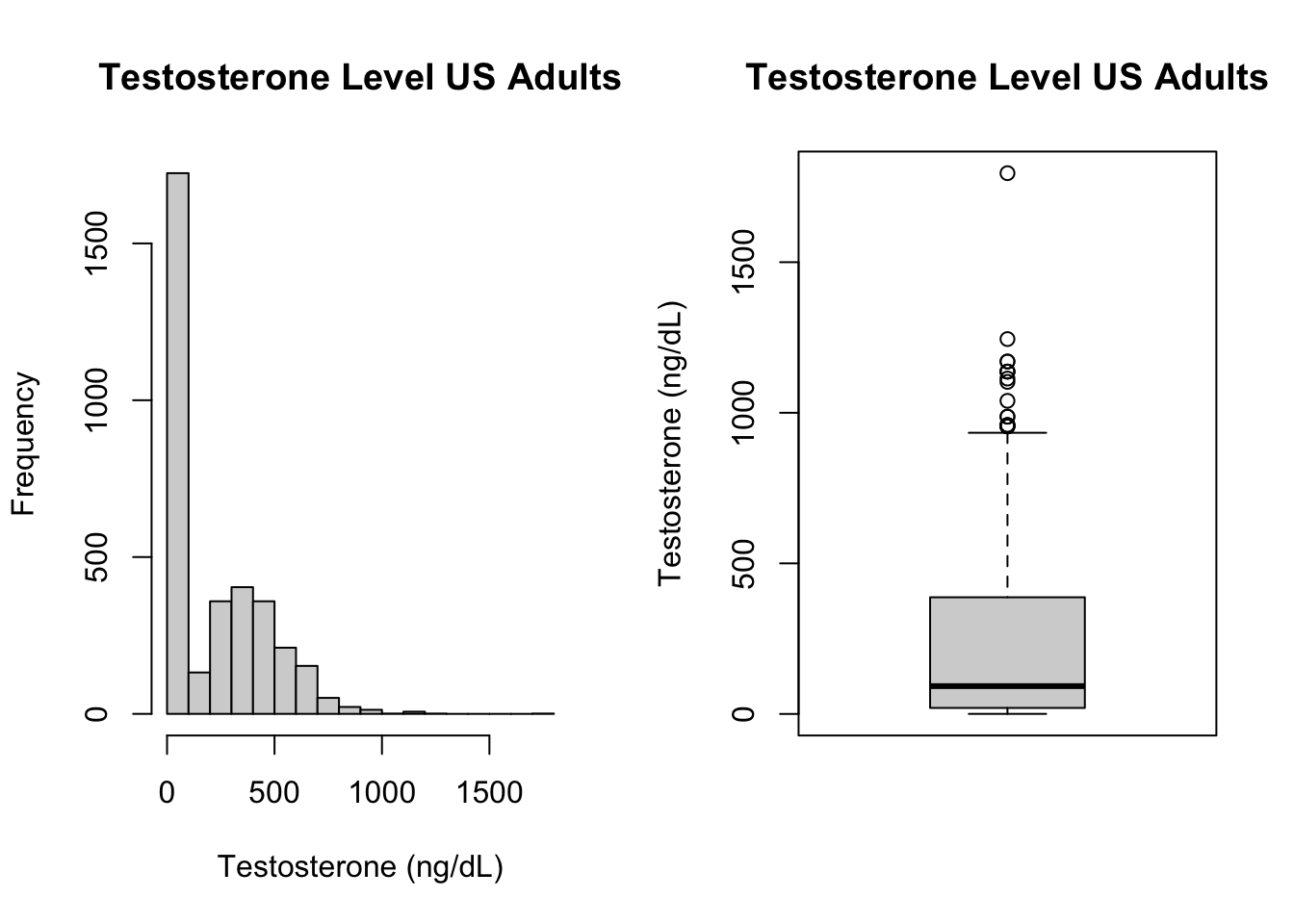

Question 3. Describe what you see here. Can you explain the strange distribution? What have we done wrong? How could we fix the problem?

1.2 Describing > 1 group

Does smoking increase your systolic blood pressure (SBP)? Do former smokers have higher SBP than non-smokers? Let’s compare smokers, non-smokers and former smokers on a few variables. Since the variable SmokeNow was only asked of people who had ever smoked more than 100 cigarettes (Smoke100), we will first need to create a new variable:

d$SmokStat[d$Smoke100 == "No"] <- "Never"
d$SmokStat[d$Smoke100 == "Yes" & d$SmokeNow == "No"] <- "Former"
d$SmokStat[d$Smoke100 == "Yes" & d$SmokeNow == "Yes"] <- "Current"

(Note: there are many ways to create new variables in R, this is one way.)

When you’ve created a new variable from existing variables, always take a moment to check that the coding worked! We use the table() function with the option useNA = "always" to see what happens with the data that is missing (“NA” in R):

table(d$Smoke100, useNA = "always")
table(d$SmokStat, useNA = "always")
table(d$Smoke100,d$SmokeNow,d$SmokStat, useNA = "always")

There were 2027 people who never smoked more than 100 cigarettes, and 1560 who did. Of those, 698 answer yes to SmokeNow, and 862 say no. 120 people did not respond to the question about ever smoking, and those are missing all 3 smoking variables. Can you identify all those numbers from the above tables?

Now let’s compare these three groups on a blood pressure. Examine the relationship between smoking status and the average of several systolic blood pressure readings (BPSysAve), first with side-by-side boxplots.

boxplot(d$BPSysAve ~ d$SmokStat, 
        main = "Systolic Blood Pressure US Adults by Smoking Status",
        ylab = "Systolic Blood Pressure (mmHg)")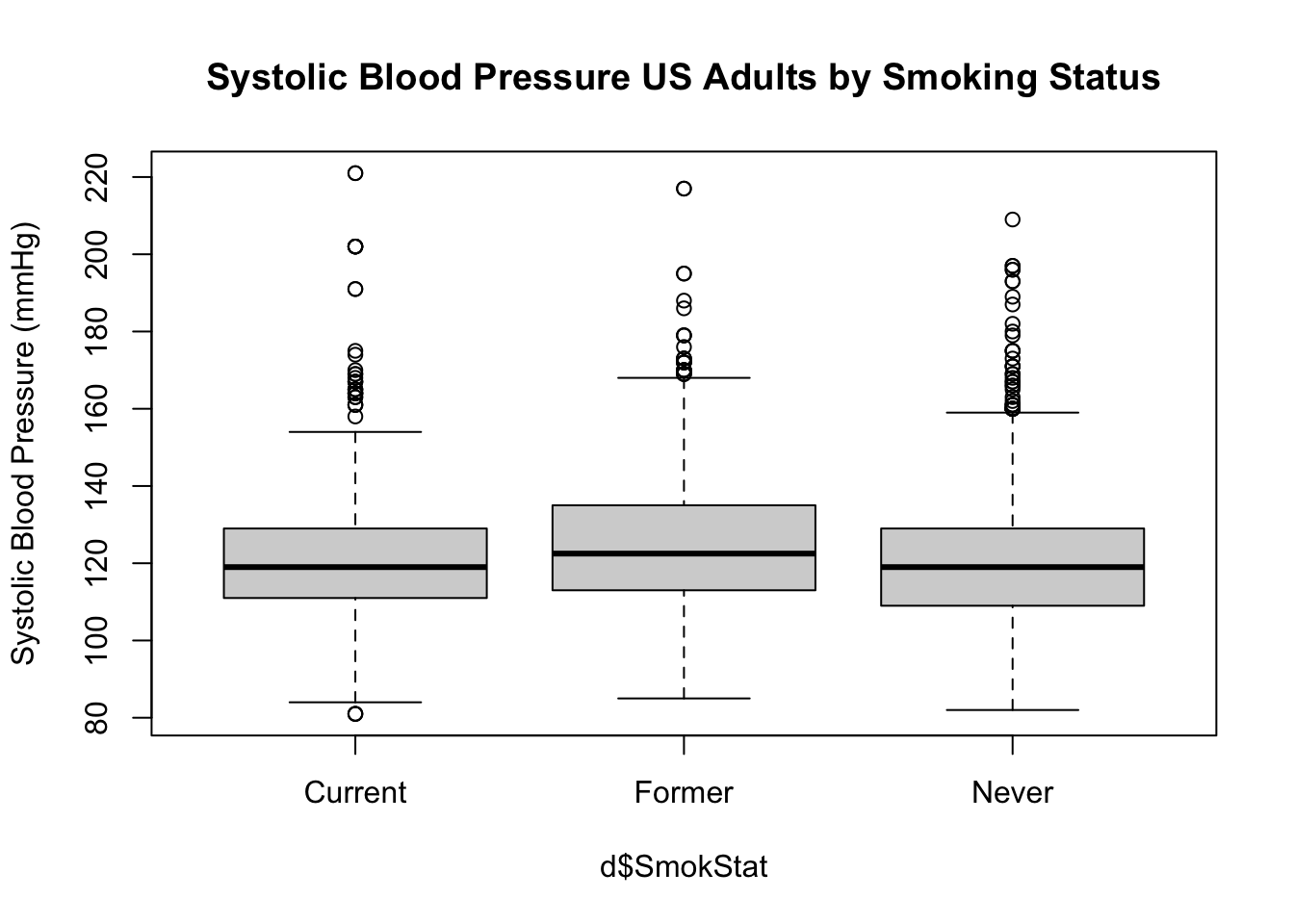

Question 4. What is the shape of the distribution for each of the groups?
Let’s get the descriptive statistics for the three groups. We’ll start by using base R functions. First we’ll get means for each group using selections:

mean(d[d$SmokStat == "Never", c("BPSysAve")], na.rm = TRUE)

## [1] 120.1813

mean(d[d$SmokStat == "Former", c("BPSysAve")], na.rm = TRUE)

## [1] 125.2447

mean(d[d$SmokStat == "Current", c("BPSysAve")], na.rm = TRUE)

## [1] 121.7299

Okay, that’s going to take too long! We could use the tapply function for the median, SD and IQR for the 3 smoking groups:

tapply(d$BPSysAve, d$SmokStat, median, na.rm = TRUE)

## Current  Former   Never 
##   119.0   122.5   119.0

tapply(d$BPSysAve, d$SmokStat, sd, na.rm = TRUE)

##  Current   Former    Never 
## 17.94236 17.95815 16.51434

tapply(d$BPSysAve, d$SmokStat, IQR, na.rm = TRUE)

## Current  Former   Never 
##      18      22      20

This goes a bit quicker, but we still need to ask for each descriptive statistic separately. We can get descriptive statistics for separate groups even faster by using the describeBy() function from the psych package. We use the same options here as we did above with the describe() function, and add the grouping variable in the group option.

describeBy(d$BPSysAve, group = d$SmokStat, na.rm = TRUE, skew = FALSE, quant = c(0.25, 0.5, 0.75), IQR = TRUE)

## 
##  Descriptive statistics by group 
## group: Current
##    vars   n   mean    sd median min max range   se IQR Q0.25 Q0.5 Q0.75
## X1    1 670 121.73 17.94    119  81 221   140 0.69  18   111  119   129
## -------------------------------------------------------------------------------------- 
## group: Former
##    vars   n   mean    sd median min max range   se IQR Q0.25  Q0.5 Q0.75
## X1    1 846 125.24 17.96  122.5  85 217   132 0.62  22   113 122.5   135
## -------------------------------------------------------------------------------------- 
## group: Never
##    vars    n   mean    sd median min max range   se IQR Q0.25 Q0.5 Q0.75
## X1    1 1953 120.18 16.51    119  82 209   127 0.37  20   109  119   129

In this way, we get all the usual descriptive statistics for SBP for each of the groups separately.

1.3 Aside: transformations

Earlier in the course you read about transformations of variables. In the NHANES dataset, HDL cholesterol was reported in mmol/L. This is the SI unit, and also the unit used to report HDL cholesterol in many countries, including the Netherlands. In the US, however, the standard units are mg/dL. The conversion factor from mmol/L to mg/dL is 38.61004. Given the following descriptive statistics for HDL cholesterol in mmol/L, can you translate the mean, median, standard deviation and IQR to mg/dL for an American physician?

##    vars    n mean   sd median  min   max range   se IQR Q0.25 Q0.5 Q0.75
## X1    1 3500    5 1.06   4.91 1.53 12.28 10.75 0.02 1.4  4.24 4.91  5.64

Now let’s check our answers by making a new variable, and getting the descriptive statistics for this new variable:

d$TotCholmgdl <- d$TotChol * 38.61004
describe(d$TotCholmgdl, na.rm = TRUE, skew = FALSE, quant = c(0.25, 0.5, 0.75), IQR = TRUE)

##    vars    n   mean    sd median   min    max  range   se   IQR  Q0.25   Q0.5  Q0.75
## X1    1 3500 193.01 40.79 189.58 59.07 474.13 415.06 0.69 54.05 163.71 189.58 217.76

Since all of the statistics we’re examining (mean, median, sd, IQR) are in the same units as the variable itself, we can multiply the descriptive statistics of TotChol to get the descriptive statistics of TotCholmgdl. Though of course making the new variable and asking for its descriptive statistics is easier (and less prone to error).

We also learned that certain transformations can help us with skewed variables. Consider, again, HDL cholesterol. Now we’ll look at direct HDL cholesterol, stored in the variable DirectChol. Get a histogram of direct HDL cholesterol:

hist(d$DirectChol)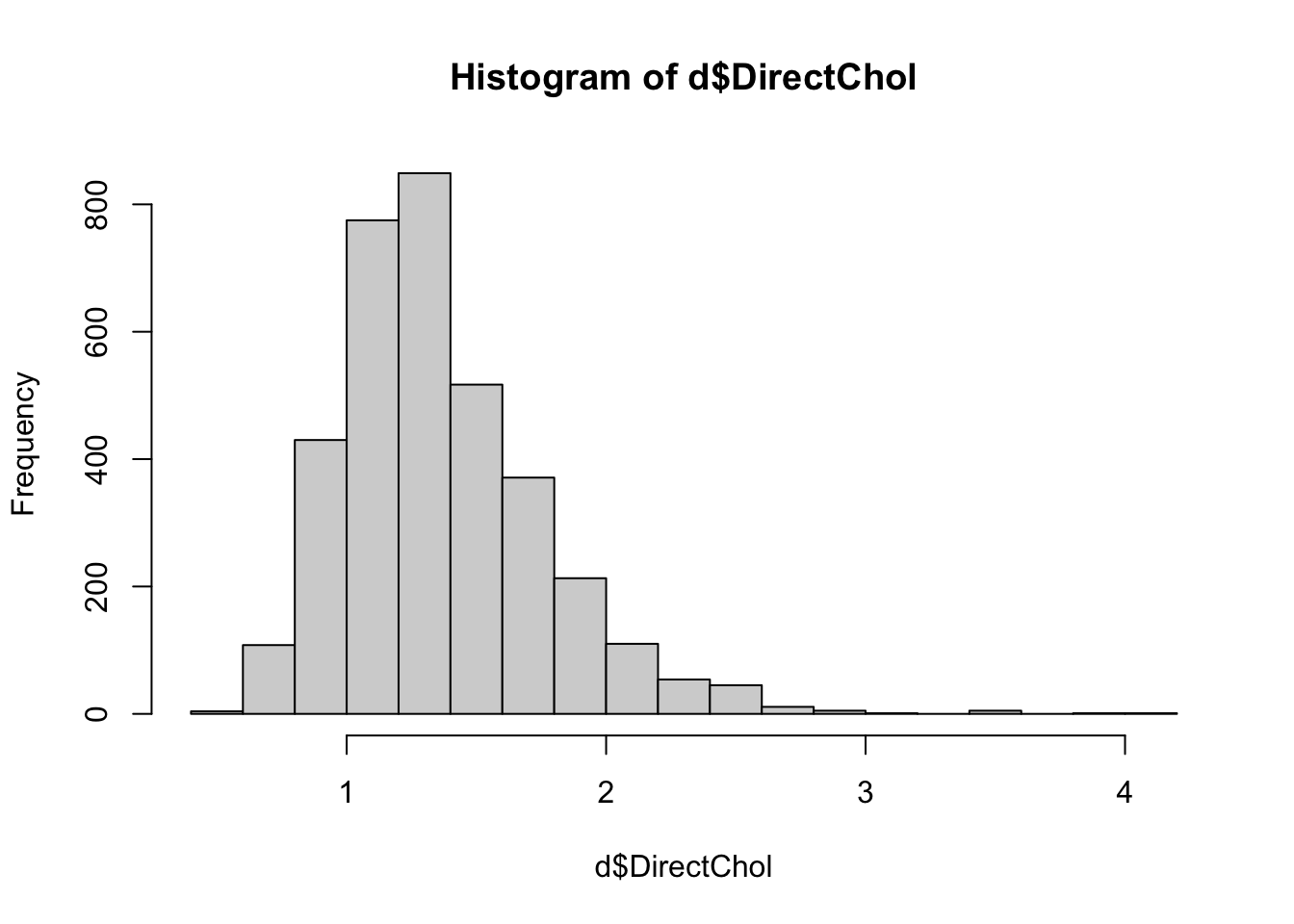

As with many other lab/physical measures variables we’ve looked at, this variable is also right-skewed. Later in the course we’ll hear more about why, but often it is useful in statistics to have (more or less) normally distributed outcome variables. A common transformation in biomedical statistics is the log transformation. Note: when statisticians say “log transformation”, we nearly always mean the “natural log transformation” (ln, or log_e), though log₁₀, log₂ or any other base will work as well. Which base you use will sometimes depend on the context of the study. However, if there is no obvious reason to choose a different base, you’ll generally see ln used (i.e. log with base e=2.718). That is the transformation we’ll use here. Make a new variable in the data frame d called lnDirChol, using log_e of DirectChol:

d$lnDirChol <- log(d$DirectChol)
hist(d$lnDirChol)

Note that in R the function log() refers to ln (if you want to use a log₁₀ transformation, use the function log10()).

Question 5. Describe the distribution of lnDirChol. What has changed after log transformation?

1.4 relationship to 1 continuous explanatory variable

Do heavier people tend to have higher blood pressure? We will examine the relationship between BMI (a continuous, numeric variable) and SBP (also a continuous, numeric variable). Though these particular variables are also available in the NHANES dataset, it might be instructive to consider a smaller sample. Often in biomedical research we do not have data from thousands of individuals at once. The file BMISBP.sav contains a sample of 40 elderly Dutch adults. Read in the data and examine the first few lines of the data frame. (Make sure you change your path name to the directory in which you have saved the file!)

d2 <- read.csv("BMISBP.csv")

dim(d2)

## [1] 40  2

head(d2)

##      BMI SBP
## 1 18.560 118
## 2 18.922 141
## 3 19.611 143
## 4 19.890 114
## 5 20.430 145
## 6 20.640 160

You have already seen how to generate scatterplots. For a quick-and-dirty examination of 2 variables at a time, the plot function in base R is generally sufficient (though much prettier plots can be made using the ggplot2 package).

plot(d2$BMI, d2$SBP)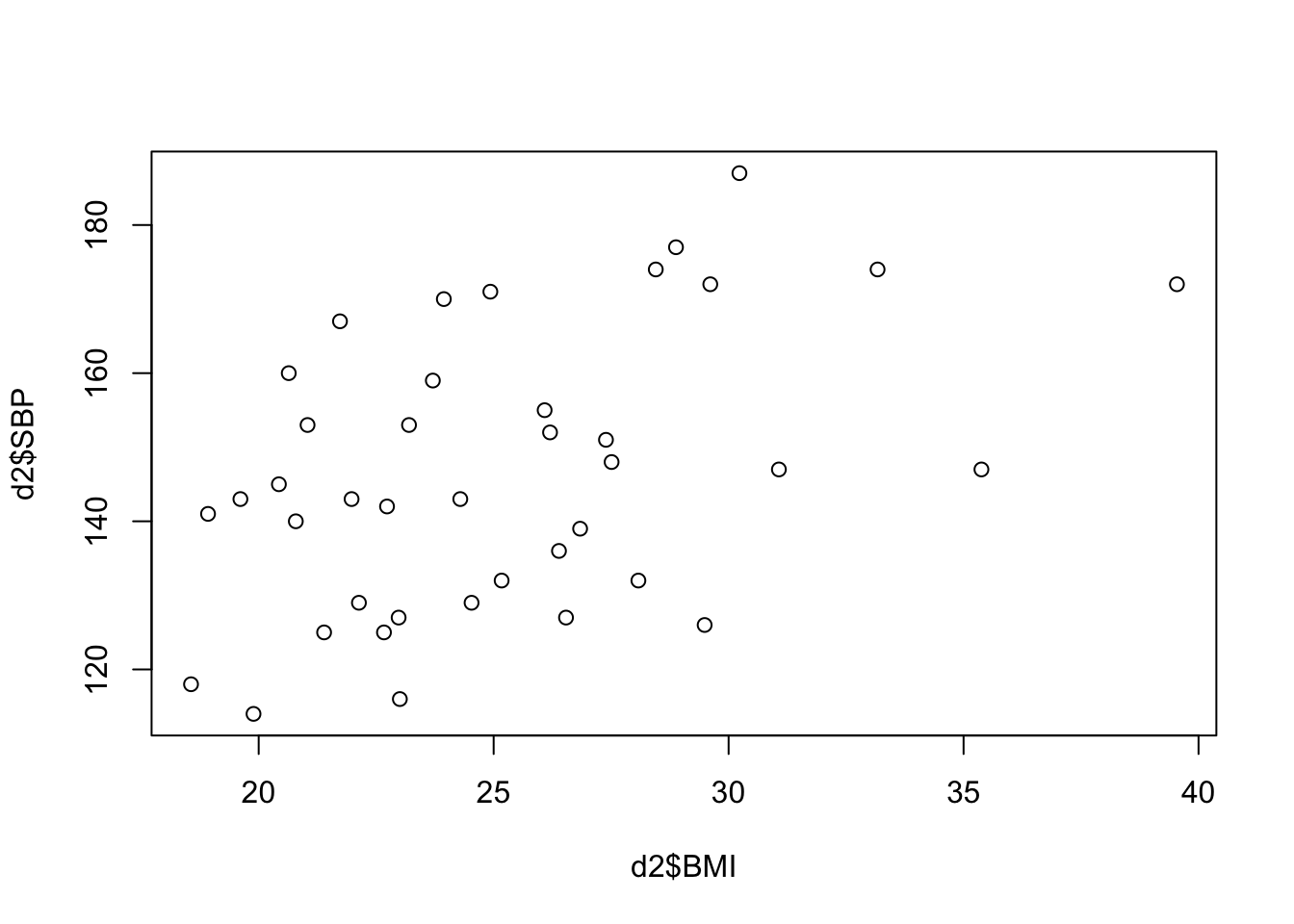

Question 6. How would you characterize the relationship between BMI and SPB? How strong do you think the correlation is?

For examining more than 2 variables, the scatterplotMatrix function in the car package can be helpful. If necessary, first install the car package. When you want to add more variables, use more + signs and add the variables you want in your scatterplot matrix.

library(car)
scatterplotMatrix(~ BMI + SBP, data = d2,  diagonal = list(method = "histogram"))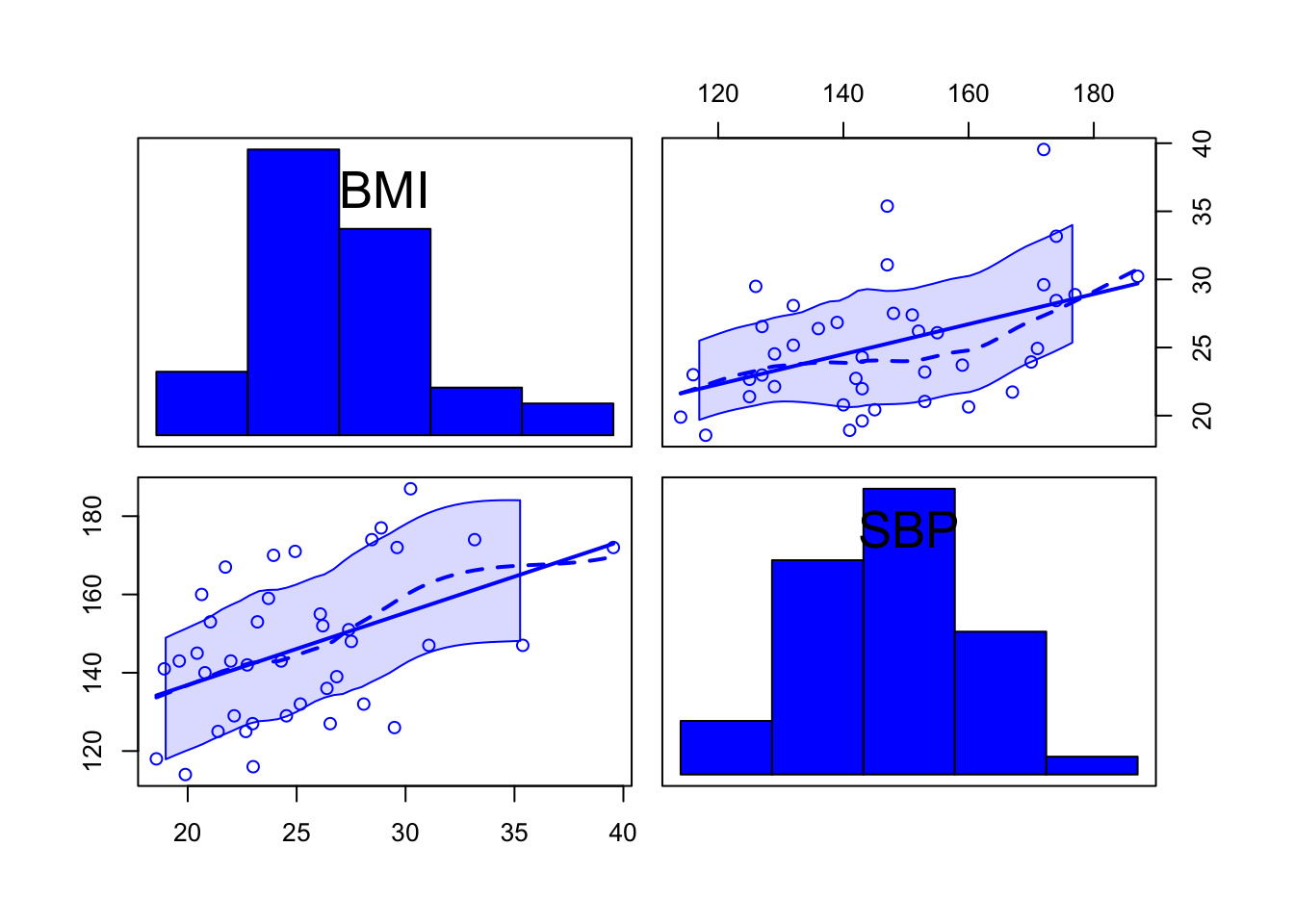

Now let’s check our guess for the correlation. Note that we need to use an option that tells R what to do with missing values in the variables examined. Since we want to look at correlations among several variables at once, we prefer to only delete the observations that are missing for the two variables being examined and therefore choose use="pairwise.complete.obs":

cor(d2$BMI, d2$SBP, use = "pairwise.complete.obs")

## [1] 0.4519469

Question 7. How does this compare to your guess? Would you call this no, weak, moderate, strong or perfect correlation?

2. Practice what you’ve learned

Now you will apply the skills you’ve learned to a new set of variables. We’ll return to the NHANES data, which should still be in the memory of R/Rstudio (if you’ve since closed RStudio and started a new session, you will need to re-run the code that read in NHANES and reduced it to the data frame d).

Using the appropriate descriptive statistics and plots, examine the distributions of, and the associations among, the following variables: age in years, the 60-second pulse rate, the combined systolic blood pressure reading, and total HDL cholesterol. Note: look again at the help function for the NHANES package to find the names of these variables.

Question 8. Describe the distributions of age, 60-second pulse rate, and total HDL cholesterol. (Since we’ve already examined SBP in detail, you may skip that)

Question 9. For which variable(s) do you expect the mean and median to be the same, and why? For which do they actually differ appreciably?

Question 10a. Examine visually and numerically the relationships among age in years, pulse rate, SBP, and HDL cholesterol. (Hint: remember the scatterplotMatrix() function.)

Question 10b. Is it reasonable to calculate correlation coefficients for these six associations?

Question 10c. Which of the six associations has the strongest correlation, and what is the correlation coefficient for that association?

Question 10d. Which of the six associations has the weakest correlation, and what is that correlation coefficient?

Question 11a. Get side-by-side boxplots and the descriptive statistics for total HDL cholesterol, separately for the body mass index categories (categorized according to WHO guidelines; this is a variable in the dataset).

Question 11b. Describe the patterns you see in HDL-c for the BMI categories.

Question 11c. Based on what you see, do you think total HDL cholesterol increases with increasing categories of BMI?