In het zelfstudiedocument is aan de hand van twee datasets een aantal toetsen behandeld: de z-toets, de t-toets en de chi-kwadraat toets. In dit COO komen deze toetsen opnieuw aan de orde, waarbij je gebruik maakt van dezelfde datasets.
In dit COO maken we gebruik van een aantal packages en functies in R. Voor het inlezen van bestanden en voor de beschrijvende statistiek zijn deze al geïntroduceerd in de COO’s over R. We verwijzen je naar deze COO’s wanneer je niet meer goed weet hoe deze functies werken. Voor de toetsen staat het benodigde R script in de betreffende vraag.
0. Voorbereiding
Zorg ervoor dat je de benodigde databestanden hebt gedownload en lokaal hebt opgeslagen:
Herinnering: open en sla dit bestand niet op met Excel (Windows) of Numbers (Mac). Zorg dat je de .csv-bestanden meteen in de goede map opslaat, of verplaats de bestanden zelf naar de juiste map zonder deze met Excel-achtige software te openen.
Het is ook handig om je ‘working directory’ te veranderen naar deze map met databestanden. Dit kun je doen via het menu: Session > Set Working Directory > Choose Directory… > selecteer de map waarin de databestanden staan. Let op: tijdens het instellen van je ‘working directory’ zie je de bestanden meestal niet staan.
Verder maken we gebruik van functies uit de BSDA en de
psych packages. Als je die nog niet hebt geïnstalleerd, doe
dat nu (install.packages("BSDA") en
install.packages("psych")). Daarna kunnen we ze laden:
library(BSDA)
library(psych)1. Spirometrie data: Z- en T-toets (stap voor stap)
In de zelfstudie is gekeken in hoeverre de FEV1 waarde van studenten verschilt van de FEV1 waarde van de Nederlandse populatie. We gebruiken hier hetzelfde voorbeeld en kijken stap-voor-stap hoe we de data kunnen beschrijven, en hoe we een z-toets en t-toets in R kunnen uitvoeren.
1.1 Data inlezen
We beginnen met het inlezen van het bestand en bekijken dit. De data
staat in een .csv-bestand spirometrie.csv. We lezen de data
in, noemen de dataframe d en bekijken de eerste rijen met
head.
d <- read.csv2("spirometrie.csv")head(d)## Student Geslacht Leeftijd Lengte Gewicht Teugvolume ERV IRV FVC FEV1 verwachtFEV1
## 1 1 V 19 174 63 1.14 0.70 1.41 3.03 3.04 3.7980
## 2 2 V 19 175 67 1.10 1.22 1.92 4.22 2.49 3.8375
## 3 3 M 21 176 60 1.31 2.09 2.10 5.02 4.58 4.4690
## 4 4 V 21 178 63 1.23 2.17 1.51 4.81 3.95 3.9060
## 5 5 M 20 196 93 0.65 2.21 3.22 6.20 5.79 5.3580
## 6 6 V 21 172 78 NA 1.65 1.51 4.36 3.91 3.66901.2 Beschrijvende statistiek
Om te beginnen worden de data in een boxplot weergegeven. Hierin is een onderscheid gemaakt tussen mannen en vrouwen. Om deze boxplot te maken kun je onderstaande code gebruiken.
Intermezzo
Je ziet in de onderstaande syntax een
tilde ~ staan. Voor de tilde staat de variabele waarin je
geïnteresseerd bent: de uitkomstvariabele (ook wel afhankelijke
variabele genoemd). Je wilt weten in hoeverre de variabele achter de
tilde iets zegt over deze uitkomstvariabele. Deze variabele noemen we de
determinant (ook wel onafhankelijke of verklarende variabele genoemd).
Deze formulering, dus y ~ x, is een algemeen gebruikte
formulering voor een model (dus hoe hangt de uitkomstvariabele samen met
de determinanten) in R en zul je bij veel statistische functies gaan
gebruiken.
boxplot(FEV1 ~ Geslacht, data = d, ylab = "FEV1 in L", xlab = "geslacht") 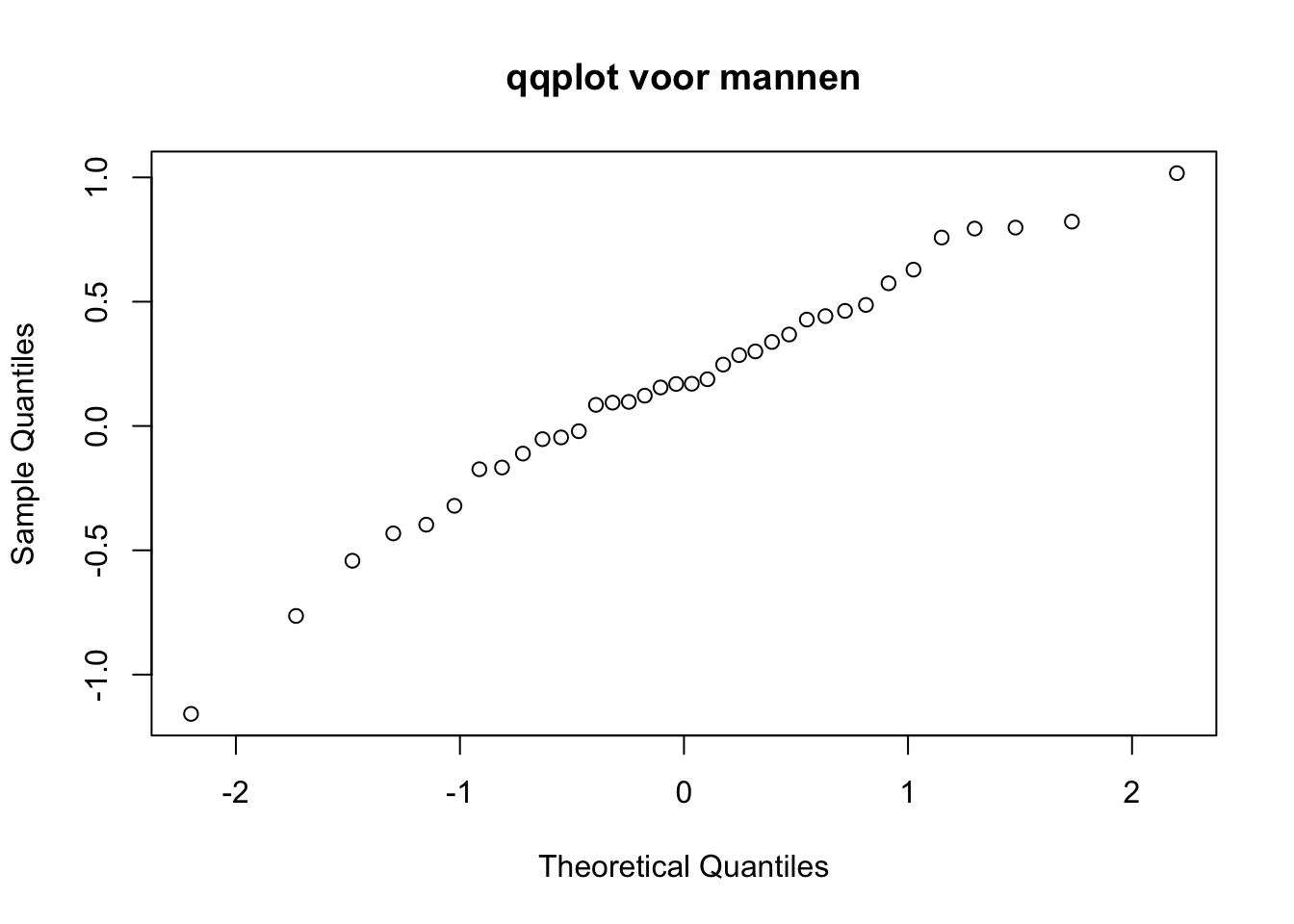
Vraag 1. Wat is je conclusie op basis van deze boxplots? Vergelijk hierbij de boxplot van de mannen en vrouwen.
Mannen hebben een hogere FEV1 waarde dan vrouwen. De spreiding in FEV1 waarden lijkt bij mannen wat groter te zijn dan bij vrouwen. Bij vrouwen is er een aantal opvallende lage waarden te zien.
Vraag 2. Lees de mediaan en interkwartielenafstand af voor de mannen en vrouwen. En schat op basis van de boxplot het gemiddelde en de standaarddeviatie.
Voor mannen zijn de schattingen op basis van de plot voor de mediaan 4.8, de IQR 0.7 (5.1 - 4.4), het gemiddelde 4.8 en de standaarddeviatie - wanneer we uitgaan van een normale verdeling - 0.5 (0.75 * 0.7). Voor vrouwen zijn de schattingen op basis van de plot voor de mediaan 3.6, de IQR 0.4 (3.8 - 3.4), het gemiddelde 3.6 en de standaarddeviatie - wanneer we uitgaan van een normale verdeling - 0.3 (0.75 * 0.4).
Om een gemiddelde FEV1 en standaarddeviatie voor mannen en vrouwen te krijgen, kunnen we een selectie uit de data maken voor mannen en vrouwen afzonderlijk en vragen om die kengetallen. Veel makkelijker: we kunnen de describeBy() functie gebruiken (we krijgen dan veel meer dan mean en SD):
describeBy(d$FEV1, group = d$Geslacht, skew = FALSE, IQR = TRUE)##
## Descriptive statistics by group
## group: M
## vars n mean sd median min max range se IQR
## X1 1 36 4.77 0.58 4.78 3.79 6.1 2.31 0.1 0.73
## ----------------------------------------------------------------------------------------------------
## group: V
## vars n mean sd median min max range se IQR
## X1 1 58 3.55 0.38 3.57 2.49 4.26 1.77 0.05 0.42Vraag 3. Komen de kengetallen die je in vraag 2 hebt afgelezen en geschat overeen met de berekende waarden?
De kengetallen komen in grote lijnen met elkaar overeen. De SD’s zijn iets groter omdat de data niet helemaal Normaal verdeeld zijn.
De FEV1 waarden zijn afhankelijk van lengte en leeftijd. In
onderstaande formules staat deze relatie voor volwassen mannen en
vrouwen weergegeven. Voor ieder van de studenten is op basis van de
lengte en leeftijd van de betreffende student de FEV1-waarde op basis
van deze formules uitgerekend. Deze variabele staat in de dataset als
verwachtFEV1 weergegeven.
Quanjer (1993)
Referentiewaarden
Vrouwen: verwachte FEV1 = 3.95H – 0.025A – 2.60
Mannen: verwachte FEV1 = 4.30H – 0.029A – 2.49
H = lengte in meters, A = leeftijd in jarenMaak nu zelf van verwachtFEV1 een boxplot en
beschrijvende statistieken voor mannen en vrouwen
boxplot(verwachtFEV1 ~ Geslacht, data = d, ylab = "verwachte FEV1 in L", xlab = "geslacht")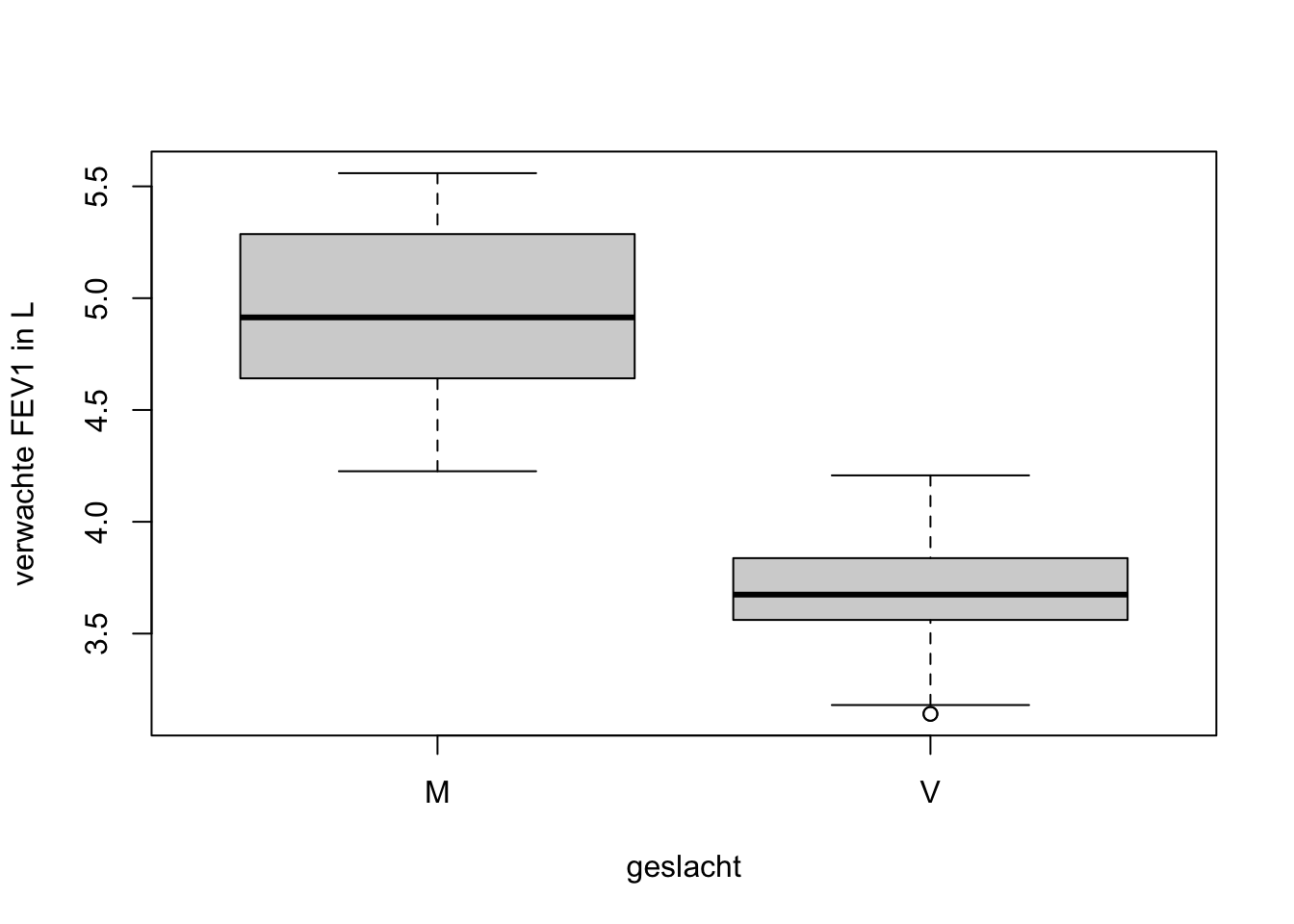
describeBy(d$verwachtFEV1, group = d$Geslacht, skew = FALSE, IQR = TRUE)##
## Descriptive statistics by group
## group: M
## vars n mean sd median min max range se IQR
## X1 1 36 4.93 0.36 4.91 4.23 5.56 1.33 0.06 0.62
## ----------------------------------------------------------------------------------------------------
## group: V
## vars n mean sd median min max range se IQR
## X1 1 58 3.68 0.25 3.67 3.14 4.21 1.07 0.03 0.28Vraag 4. Vergelijk nu ook de resultaten van de mannen en vrouwen. Zijn je conclusies hetzelfde als bij vraag 1?
Zowel bij de mannen als bij de vrouwen lijkt de verdeling wat meer symmetrisch te zijn. Verder komen de conclusies overeen.
1.3 Z-toets voor een gemiddelde
We willen weten of de FEV1 van de studenten overeen komt met de FEV1 van de Nederlandse populatie. Om rekening te houden met lengte en leeftijd zijn verwachte FEV1 waardes berekend. Als de nulhypothese waar zou zijn (er is geen gemiddeld verschil), dan verwacht je dat gemiddeld genomen het verschil tussen de geobserveerde en de verwachte FEV1 0 is.
Bereken het verschil tussen de geobserveerde FEV1 en de verwachte FEV1 met behulp van de code hieronder.
d$verschil <- d$verwachtFEV1 - d$FEV1Om een z- of t-toets te gebruiken, veronderstellen we dat de data normaal verdeeld zijn.
Maak met onderstaande code de boxplots en histogrammen
waarmee je kunt beoordelen in hoeverre je voldoet aan de aanname van
normaliteit. Je houd hierbij rekening met mogelijke verschillen in
geslacht. Naast deze plots, is het gebruikelijk om een ‘normal
probability plot’ te gebruiken voor het beoordelen van normaliteit van
de data. Deze plot is al geïntroduceerd in Oog voor Impact (voor
opfrissen: zie PSLS hoofdstuk 11, paragraaf ‘Normal quantile plots’). Om
een normal probability plot te maken, gebruik je de functies
qqnorm() en qqline(). Voor de mannen:
qqnorm(d$verschil[d$Geslacht == "M"], main = "qqplot voor mannen")
qqline(d$verschil[d$Geslacht == "M"])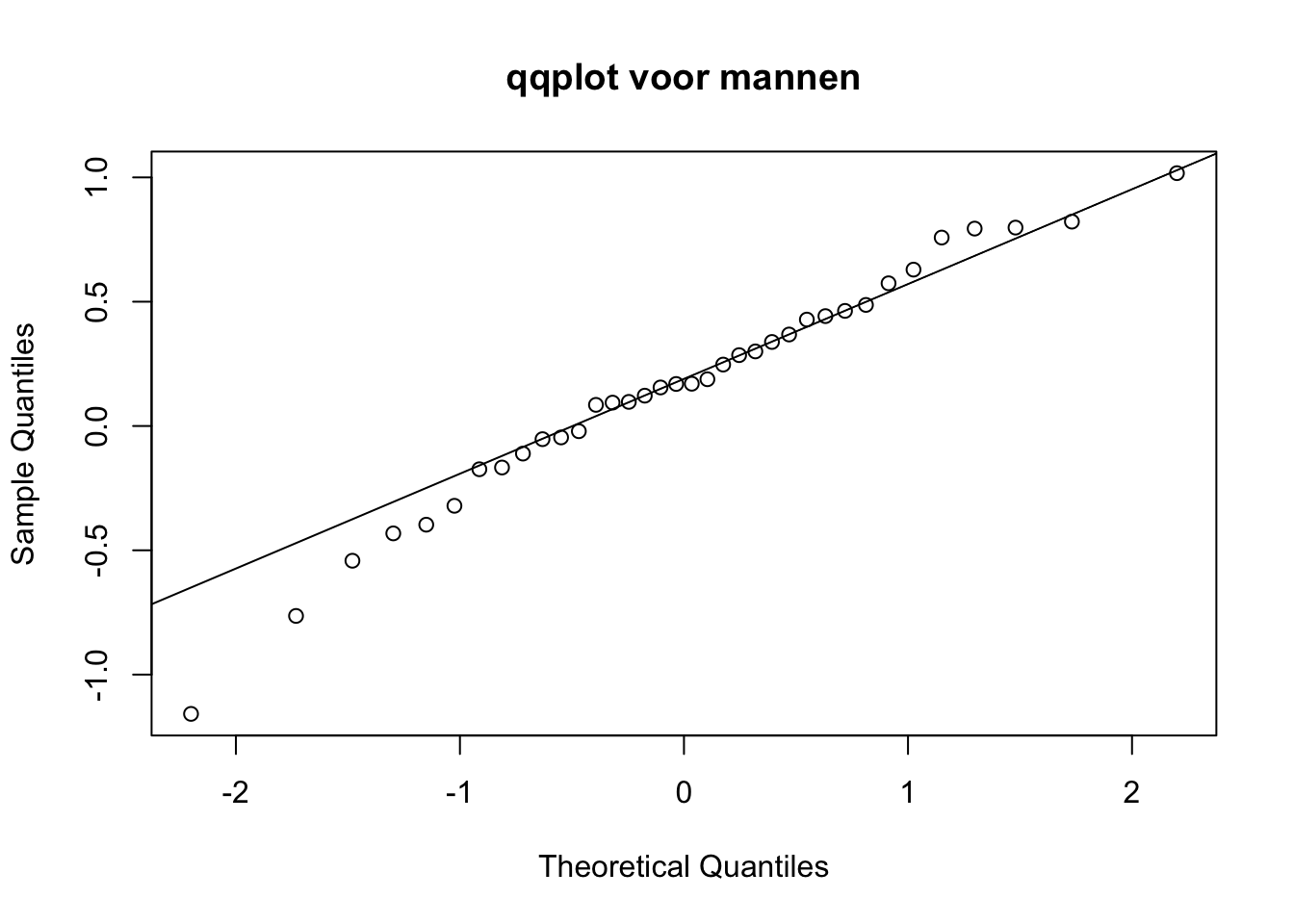
Maak nu zelf een normal probability plot voor de FEV1 voor de vrouwen.
qqnorm(d$verschil[d$Geslacht == "V"], main = "qqplot voor vrouwen")
qqline(d$verschil[d$Geslacht == "V"])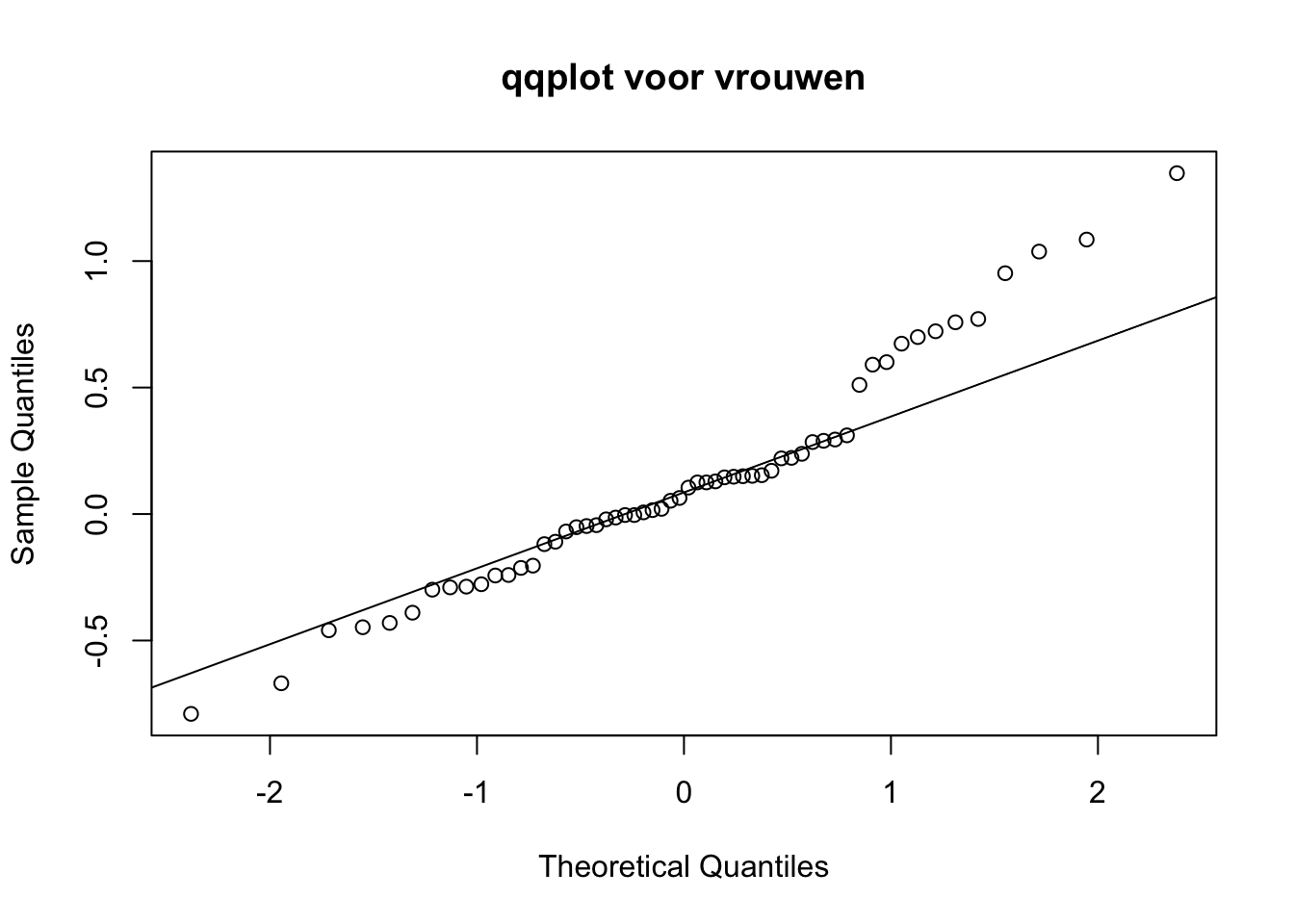
Vraag 5. Wat is op basis van de gemaakte plots jouw conclusie ten aanzien van de normaliteit van de data?
De plots passen bij de aanname van normaliteit van de data.
In eerste instantie mag je veronderstellen dat de standaard deviatie
van de populatie bekend is, en wel gelijk aan 0.5. Verder
ga je er vanuit dat de data normaal verdeeld zijn. Je wil \(H_0:\mu = 0\) en \(H_1:\mu \neq 0\) toetsen.
In R is er in de package BSDA een z-toets beschikbaar.
Als je die nog niet hebt geïnstalleerd, doe dat nu met de functie
install.packages("BSDA"). Wil je de z-waarde uitrekenen in
R, dan gaat dit als volgt. Voor de mannen:
z.test(d$verschil[d$Geslacht == "M"],
sigma.x = 0.5,
alternative = "two.sided",
mu = 0,
conf.level = 0.95)Standaard in R is de waarde voor \(\mu\) gelijk aan 0. Ook
default wordt er een tweezijdig 95%-betrouwbaarheidsinterval geschat.
Dus mu = 0, alternative = "two.sided", conf.level = 0.95 is
in het R script niet nodig om de toets te laten uitvoeren, maar is nu
voor de volledigheid wel vermeld.
Voer, zowel voor de mannen als voor de vrouwen afzonderlijk, een z-toets uit.
z.test(d$verschil[d$Geslacht == "M"],
sigma.x = 0.5,
alternative = "two.sided",
mu = 0,
conf.level = 0.95)##
## One-sample z-Test
##
## data: d$verschil[d$Geslacht == "M"]
## z = 1.8813, p-value = 0.05993
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.006552554 0.320108110
## sample estimates:
## mean of x
## 0.1567778z.test(d$verschil[d$Geslacht == "V"],
sigma.x = 0.5,
alternative = "two.sided",
mu = 0,
conf.level = 0.95)##
## One-sample z-Test
##
## data: d$verschil[d$Geslacht == "V"]
## z = 1.9544, p-value = 0.05066
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.0003675948 0.2569882845
## sample estimates:
## mean of x
## 0.1283103Vraag 6. Wat is je conclusie ten aanzien van de onderzoeksvraag?
We hebben als nulhypothese getoetst dat er geen verschil is in gemiddelde FEV1 van de mannelijke studenten ten opzichte van de Nederlandse mannelijke populatie (normwaarde). De gevonden p-waarde is 0.05993 en hiermee verwerpen we de nulhypothese niet. Er is inderdaad geen aanwijzing gevonden dat de gemiddelde FEV1 van mannelijke studenten verschilt van de Nederlandse mannelijke populatie. Het bijbehorende 95% betrouwbaarheidsinterval is [-0.007; 0.320].
Wanneer we de gemiddelde FEV1 van de vrouwelijke studenten toetsen, dan is het verschil met de Nederlandse vrouwelijke populatie ook niet significant (p-waarde is 0.05066). Het bijbehorende betrouwbaarheidsinterval is [-0.0004; 0.257].
1.4 T-toets voor een gemiddelde
In de vorige paragraaf hebben we aangenomen dat de populatie standaard deviatie bekend was. Met deze aanname konden we gebruik maken van een z-toets. In de praktijk kennen we deze populatie standaard deviatie meestal niet. Om dan een toets op het populatie gemiddelde te doen, maken we gebruik van een t-toets. Ook hier veronderstellen we dat de data normaal verdeeld zijn. Deze aanname hebben we in de vorige paragraaf al gecontroleerd.
De t-toets is onderdeel van de basis van R, je hebt hier geen aparte package voor nodig. Voor de mannen ziet het script er als volgt uit:
t.test(d$verschil[d$Geslacht == "M"],
mu = 0,
alternative = "two.sided",
conf.level = 0.95)Ook nu zijn de standaard waardes mu = 0,
alternative = "two.sided" en
conf.level = 0.95.
Voer een t-toets uit voor zowel mannen als vrouwen.
t.test(d$verschil[d$Geslacht == "M"],
mu = 0,
alternative = "two.sided",
conf.level = 0.95)##
## One Sample t-test
##
## data: d$verschil[d$Geslacht == "M"]
## t = 2.0183, df = 35, p-value = 0.05128
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.000917816 0.314473372
## sample estimates:
## mean of x
## 0.1567778t.test(d$verschil[d$Geslacht == "V"],
mu = 0,
alternative = "two.sided",
conf.level = 0.95)##
## One Sample t-test
##
## data: d$verschil[d$Geslacht == "V"]
## t = 2.2522, df = 57, p-value = 0.02818
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.01422853 0.24239215
## sample estimates:
## mean of x
## 0.1283103Vraag 7. Verandert je conclusie ten aanzien van de nulhypothese voor mannen en vrouwen nu je een t-toets gebruikt? En als je conclusie verandert, kun je dan aangeven welke parameter hiervoor verantwoordelijk is?
Voor de mannelijke studenten is de gevonden p-waarde nu 0.05128 met een 95%-betrouwbaarheidsinterval van [-0.0009; 0.314] en verandert de conclusie niet. Voor de vrouwelijke studenten is de gevonden p-waarde nu 0.02818 met een 95%-betrouwbaarheidsinterval van [0.014; 0.242] en concluderen we dat de vrouwelijke studenten gemiddeld genomen een lagere FEV1 hebben dan de Nederlandse vrouwelijke populatie.
De standaarddeviaties in de steekproef zijn kleiner dan de in de
z-toets veronderstelde 0.5. Daardoor wordt de waarde van de
toetsingsgrootheid groter en de p-waarde lager.
LET OP: wanneer we de standaarddeviatie uit de steekproef hadden
gebruikt in de z-toets, dan waren de p-waardes van de t-toets hoger
geweest dan die van de z-toets!!
In het databestand spirometrie staan ook de variabelen lengte en
gewicht. Bereken de BMI (gewicht [in kg])/(lengte [in m])\(^2\). De gemiddelde BMI voor volwassen
mannen is in Nederland 26.9 en voor volwassen vrouwen
26.6.
Vraag 8. Toets of de studenten gemiddeld genomen een lagere
BMI hebben dan de gemiddelde Nederlandse BMI. Houd hierbij rekening met
de variabele Geslacht. Gebruik het stappenplan voor
toetsen.
d$BMI <- d$Gewicht/((d$Lengte*0.01)^2)Stap 1 – Formuleer
Als onderzoeksvraag is gesteld: is de gemiddelde BMI van studenten lager
dan de gemiddelde BMI van de gehele volwassen Nederlandse populatie? In
deze onderzoeksvraag wordt rekening gehouden met de variabele geslacht,
omdat de gemiddelde BMI afhankelijk blijkt te zijn van geslacht.
Stap 2 – Ontwerp
Om het gemiddelde van beide groepen studenten te toetsen, gebruik je een
één steekproef t-toets. Immers, de standaarddeviatie is onbekend en
schat je ook uit de steekproef. Daarmee is een z-toets niet van
toepassing. Bij het gebruik van een t-toets veronderstel je dat de data
normaal verdeeld zijn en onafhankelijk van elkaar. Voor de mannen zijn
de hypotheses: H₀:μ=26.9 vs H₁:μ<26.9. Voor de vrouwen zijn de
hypotheses: H₀:μ=26.6 vs H₁:μ<26.6.
Stap 3 – Pas toe
Allereerst controleer je of de data voldoen aan de aanname van
normaliteit. De aanname van onafhankelijkheid kun je niet controleren
met het databestand, dit moet worden gegarandeerd door de wijze waarop
het onderzoek is opgezet. Voor het controleren van de aannames maak je
een aantal plots.
par(mfrow=c(2,3))
boxplot(d$BMI ~ d$Geslacht, xlab="Geslacht", ylab="BMI")
hist(d$BMI[d$Geslacht=="M"], xlab="BMI")
hist(d$BMI[d$Geslacht=="V"], xlab="BMI")
qqnorm(d$BMI[d$Geslacht=="M"], main="qqplot voor mannen")
qqline(d$BMI[d$Geslacht=="M"])
qqnorm(d$BMI[d$Geslacht=="V"], main="qqplot voor vrouwen")
qqline(d$BMI[d$Geslacht=="V"])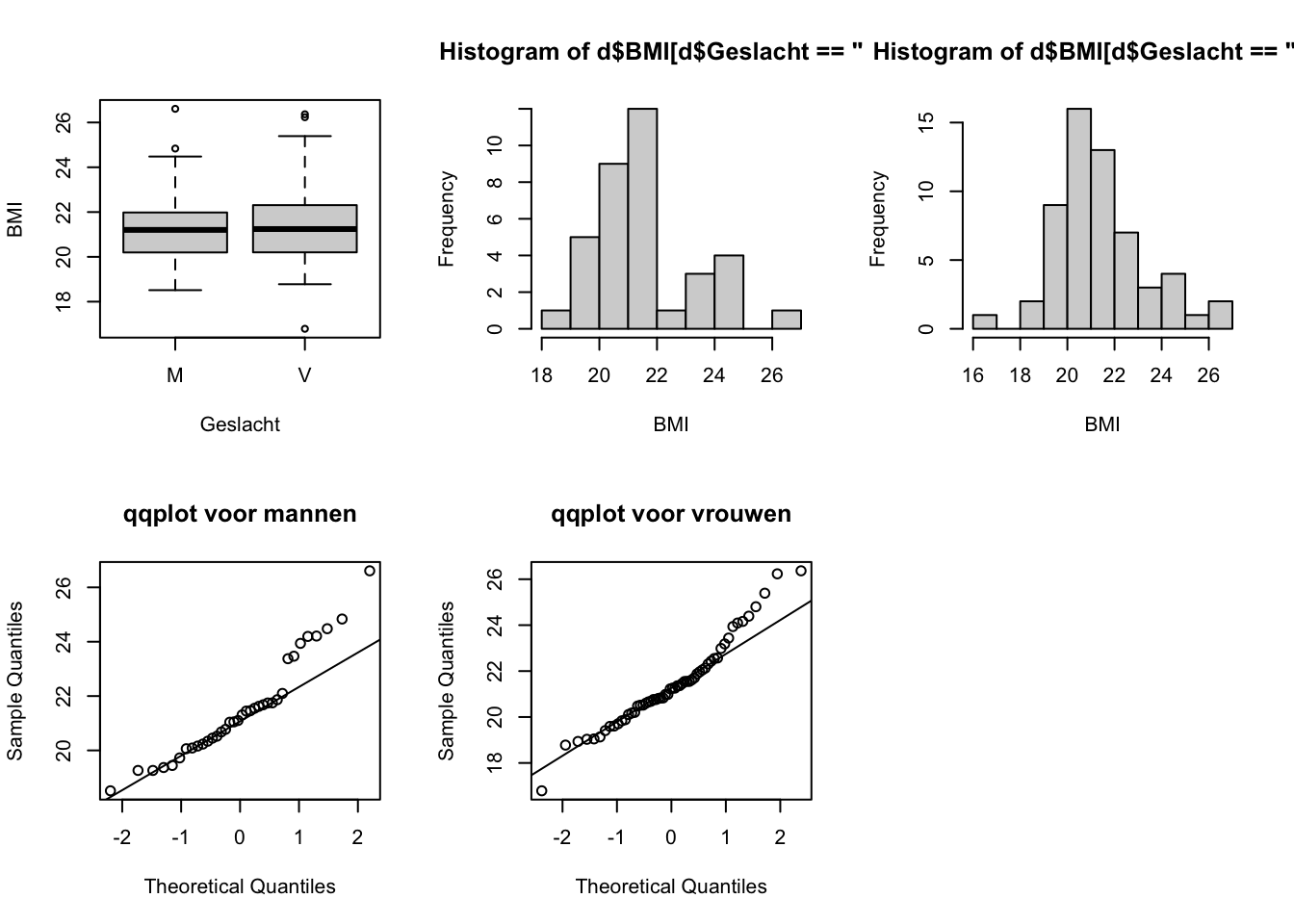
Gebaseerd op de plots is er geen directe aanleiding om te twijfelen aan de aanname van normaliteit, in ieder geval bij de vrouwen niet.
Vervolgens voer je een t-toets uit. Deze is eenzijdig en dat kun je aangeven in R.
t.test(d$BMI[d$Geslacht == "M"],
mu = 26.9,
alternative = "less",
conf.level = 0.95)##
## One Sample t-test
##
## data: d$BMI[d$Geslacht == "M"]
## t = -17.655, df = 35, p-value < 2.2e-16
## alternative hypothesis: true mean is less than 26.9
## 95 percent confidence interval:
## -Inf 22.00952
## sample estimates:
## mean of x
## 21.49199t.test(d$BMI[d$Geslacht == "V"],
mu = 26.6,
alternative = "less",
conf.level = 0.95)##
## One Sample t-test
##
## data: d$BMI[d$Geslacht == "V"]
## t = -20.981, df = 57, p-value < 2.2e-16
## alternative hypothesis: true mean is less than 26.6
## 95 percent confidence interval:
## -Inf 21.83363
## sample estimates:
## mean of x
## 21.4209Stap 4 – Concludeer
Op basis van deze output is je conclusie als volgt: zowel voor de mannen
als de vrouwen vind je een heel kleine p-waarde (<2.2e-16). Dit
betekent dat beide nulhypotheses worden verworpen: zowel de mannelijke
als vrouwelijke studenten hebben gemiddeld een lagere BMI dan het
landelijke gemiddelde.
2. SARS-CoV-2 en bloedgroep data: chi-kwadraat toets (stap voor stap)
In de zelfstudie is gekeken naar een onderzoek waarin werd onderzocht of er een relatie is tussen de ABO-bloedgroepen en infecties met corona (Ellinghaus et al, 2020, Genomewide Association Study of Severe Covid-19 with Respiratory Failure | NEJM). Ook met deze dataset ga je de analyse in R uitvoeren. We gebruiken hiervoor de oorspronkelijke dataset uit het artikel.
2.1 Data invoeren
Maak deze dataset aan in R met behulp van onderstaande code:
d <- matrix(c(398, 25, 65, 462, 377, 36, 71, 291), 4)
rownames(d) <- c("A", "AB", "B", "O")
colnames(d) <- c("controls", "cases")Om R de matrix als een frequentie tabel te laten zien, is er nog een
extra stap nodig: gebruik hiervoor de functie
as.table().
dtab <- as.table(d)
dtab## controls cases
## A 398 377
## AB 25 36
## B 65 71
## O 462 2912.2 Beschrijvende statistiek
Voor de interpretatie van de studie is het inzichtelijker om de frequenties niet als absolute, maar als relatieve (of procentuele) frequenties weer te geven.
Maak met onderstaande code een tabel met relatieve frequenties:
# Met de onderstaande functie krijg je de frequenties voor alle bloedgroepen en controles en patiënten samen.
proptab0 <- prop.table(dtab)
proptab0## controls cases
## A 0.23072464 0.21855072
## AB 0.01449275 0.02086957
## B 0.03768116 0.04115942
## O 0.26782609 0.16869565# Toevoegen van '1' geeft aan dat de frequenties worden berekend over de rijen.
proptab1 <- prop.table(dtab, 1)
proptab1## controls cases
## A 0.5135484 0.4864516
## AB 0.4098361 0.5901639
## B 0.4779412 0.5220588
## O 0.6135458 0.3864542# Toevoegen van '2' geeft aan dat de frequenties worden berekend over de kolommen.
proptab2 <- prop.table(dtab, 2)
proptab2## controls cases
## A 0.41894737 0.48645161
## AB 0.02631579 0.04645161
## B 0.06842105 0.09161290
## O 0.48631579 0.37548387Vraag 9. Welke informatie krijg je met de verschillende relatieve frequenties die je kunt berekenen? Welke relatieve frequenties hebben jouw voorkeur bij de interpretatie?
prop.table(dtab) geeft relatieve frequenties ten
opzichte van het totaal aantal deelnemers,
prop.table(dtab,1) geeft relatieve frequenties per
bloedgroep en prop.table(dtab,2) geeft relatieve
frequenties per ‘corona’-groep. Wanneer we beide ‘corona’-groepen met
elkaar willen vergelijken, dan zijn de relatieve frequenties per groep
het meest informatief.
2.3 Chi-kwadraat toets
Om de vraag van de onderzoekers te beantwoorden, voeren we een chi-kwadraat toets uit.
Vraag 10. Welke hypotheses formuleer je op basis van de onderzoeksvraag?
Met de chi-kwadraat toets toetsen we als nulhypothese dat er geen associatie is tussen bloedgroep en het wel of niet hebben van corona. De alternatieve hypothese is dan dat er wel een associatie is.
Voer een chi-kwadraat toets uit op de data met onderstaande code:
dtest <- chisq.test(dtab)
dtestdtest bevat alle resultaten van
chisq.test(dtab), waaronder ook de verwachte frequenties
onder de nulhypothese. Je kunt deze verwachte frequenties opvragen
met:
dtest$expectedVraag 11. Wat is op basis van je analyse je conclusie ten aanzien van de onderzoeksvraag (betrek hierbij ook de verwachte frequenties)?
Op basis van de p-waarde verwerpen we de nulhypothese. We zien dat bloedgroep O minder vaak voorkomt bij de mensen met corona dan verwacht en bloedgroepen A, B en AB vaker.
3. Progeria data invoeren en analyseren
Bij een kind met de genetische aandoening Progeria wordt het lichaam
snel ouder. Een groot deel van de kinderen met Progeria overlijdt jong,
in de tienerjaren, aan cardiovasculaire aandoeningen. In een klinische
studie wordt een aantal fysiologische variabelen, waaronder de
polsgolfsnelheid (PWV, Pulse Wave Velocity), onderzocht. De PWV wordt
vaak gebruikt als maat voor de vasculaire stijfheid, welke samenhangt
met de cardiovasculaire gezondheid van een individu. Wanneer de PWV
boven de 6.6 m/s komt, spreekt men van een abnormaal hoge
PWV. De onderzoekers vragen zich af of bij kinderen met Progeria deze
PWV waarde ook abnormaal hoog is. De onderzoekers hebben de volgende PWV
waarden gevonden:
## 18.8 17.6 17.5 16 17.8 14.1 13.7 13.1 12.9 12.9 12.4 10.1 9.3 9.1 8.3 8.3 7.9 7.2Doorloop het 4-stappenplan voor toetsen. Voer de analyse uit in R.
d <- c(18.8, 17.6, 17.5, 16.0, 17.8, 14.1, 13.7, 13.1, 12.9, 12.9, 12.4, 10.1, 9.3, 9.1, 8.3, 8.3, 7.9, 7.2)
describe(d)## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 18 12.61 3.82 12.9 12.56 5.49 7.2 18.8 11.6 0.14 -1.46 0.9par(mfrow=c(1,3))
boxplot(d)
hist(d)
qqnorm(d)
qqline(d)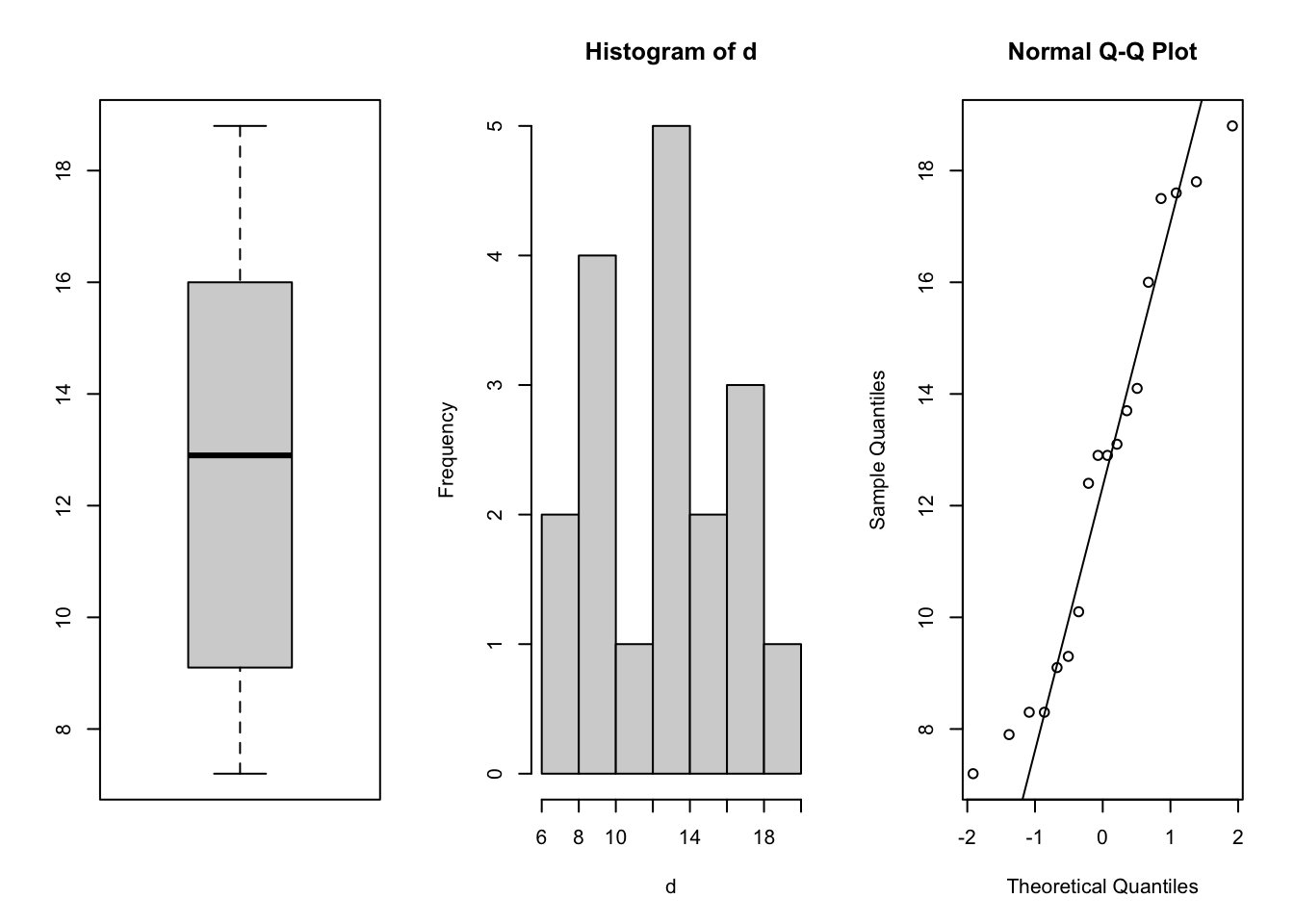
Stap 1 – Formuleer:
In dit onderzoek wil men weten in hoeverre de PWV waarde van kinderen
met Progeria abnormaal hoog is. PWV is één van de parameters die de
cardiovasculaire gezondheid van een individu weerspiegelt.
Stap 2 – Ontwerp:
De individuele PWV waarden variëren; we veronderstellen dat deze waarden
normaal verdeeld zijn. We schatten zowel het gemiddelde als de
standaarddeviatie uit de steekproef. We toetsen het populatiegemiddelde.
Onze nulhypothese is H₀: μ=6.6 (of H₀: μ≤6.6) en onze alternatieve
hypothese is H₁: μ>6.6. We toetsen de nulhypothese met een t-toets
voor één steekproef. We toetsen met een onbetrouwbaarheid van 5%.
Stap 3 – Pas toe:
Je controleert allereerst of de data voldoen aan de aanname van een
normale verdeling. Hiertoe voer je de data in R in en maken we
plaatjes.
De data geven geen aanleiding om te twijfelen aan de aanname van normaliteit in de populatie. Er zijn geen extreme uitbijters.
t.test(d, alternative = c("greater"), mu = 6.6, conf.level = 0.95)##
## One Sample t-test
##
## data: d
## t = 6.6825, df = 17, p-value = 1.928e-06
## alternative hypothesis: true mean is greater than 6.6
## 95 percent confidence interval:
## 11.04629 Inf
## sample estimates:
## mean of x
## 12.61111Vraag 12. Wat is je conclusie ten aanzien van de onderzoeksvraag?
Stap 4 – Concludeer:
De p-waarde is ‘1.501e-06’, dit is gelijk aan 0.000001501. Deze p-waarde
is veel kleiner dan de onbetrouwbaarheid van 5%. Je verwerpt de
nulhypothese en concludeert dat de gemiddelde PWV waarde bij kinderen
met Progeria abnormaal hoog is.
Veel programma’s geven niet de mogelijkheid om aan te geven of je één- of tweezijdig toetst: de berekeningen zijn dan gebaseerd op een tweezijdige toets.
t.test(d, mu = 6.6, conf.level = 0.95)##
## One Sample t-test
##
## data: d
## t = 6.6825, df = 17, p-value = 3.855e-06
## alternative hypothesis: true mean is not equal to 6.6
## 95 percent confidence interval:
## 10.71328 14.50894
## sample estimates:
## mean of x
## 12.61111Vraag 13. Hoe kun je met dergelijke output dan toch éénzijdig toetsen?
Wanneer je een tweezijdige alternatieve hypothese gebruikt, dan kijk je eerst of het gevonden steekproefgemiddelde in de richting van de alternatieve hypothese ligt. In dit geval is het steekproefgemiddelde 12.44444, dat is zeker in de richting van de alternatieve hypothese (H₁: μ>6.6). Is het steekproefgemiddelde in de richting van de alternatieve hypothese, dan deel je de gevonden p-waarde (dit is een tweezijdige p-waarde) door twee: 3.002e-06/2 = 1.501e-06. Deze p-waarde is kleiner dan de onbetrouwbaarheid van 5% en dus verwerp je de nulhypothese. Wanneer het gevonden steekproefgemiddelde niet in de richting ligt van de alternatieve hypothese (in dit voorbeeld zou het steekproefgemiddelde dan kleiner zijn dan 6.6), dan weet je zeker dat je de nulhypothese niet gaat verwerpen. De p-waarde zal dan groter zijn dan 0.5. Om deze exact uit te rekenen deel je de tweezijdige p-waarde ook door twee en trek je dit getal af van 1.
4. Paracetamol data inlezen en analyseren
In een paracetamol tablet zit – volgens de verpakking – 500 mg
paracetamol. Deze hoeveelheid paracetamol is variabel, dat wil zeggen:
in een tablet zal nooit exact 500 mg paracetamol zitten. De vraag is nu
of de fabrikant van de tabletten doet wat er wordt beloofd. Is de
hoeveelheid paracetamol in een steekproef van tabletten gelijk aan 500
mg? In het bestand paracetamol.csv vind je metingen van een
practicum van een eerder studiejaar. Er zijn twee metingen met UV en
twee metingen met HPLC uitgevoerd. Als uitkomstvariabele gebruik je het
gemiddelde van de twee UV-metingen.
Doorloop het 4-stappenplan voor toetsen voor deze dataset. Voer de analyse uit in R.
d <- read.csv("Werkcollege_statistiek_Thema_3/paracetamol.csv", sep=";", dec=",")Stap 1 – Formuleer
De onderzoekers willen weten of een fabrikant doet wat hij belooft: zit
er gemiddeld genomen inderdaad 500 mg paracetamol in een tablet of niet?
De onderzoekers zijn geinteresseerd in afwijkingen zowel naar beneden
(omdat een fabrikant zo min mogelijk werkzame stof in zijn tabletten wil
stoppen – de tabletten worden hiermee goedkoper) als naar boven (te veel
werkzame stof zou mogelijk toxisch zijn).
Stap 2 – Ontwerp
De onderzoekers gaan uit de steekproef een gemiddelde en
standaarddeviatie berekenen. Ze willen het gemiddelde toetsen. Wanneer
ze uitgaan van een normale verdeling van de hoeveelheid paracetamol, dan
kunnen ze een één steekproef t-toets gebruiken. De hypotheses worden
dan: H₀: μ=500 en H₁: μ≠500.
Stap 3 – Pas toe
We lezen eerst de data in.
Allereerst controleren de onderzoekers de aannames van de toets.
par(mfrow=c(1,3))
boxplot(d$Gem.UV)
hist(d$Gem.UV, xlab="paracetamol hoeveelheid (UV)", main="")
qqnorm(d$Gem.UV)
qqline(d$Gem.UV)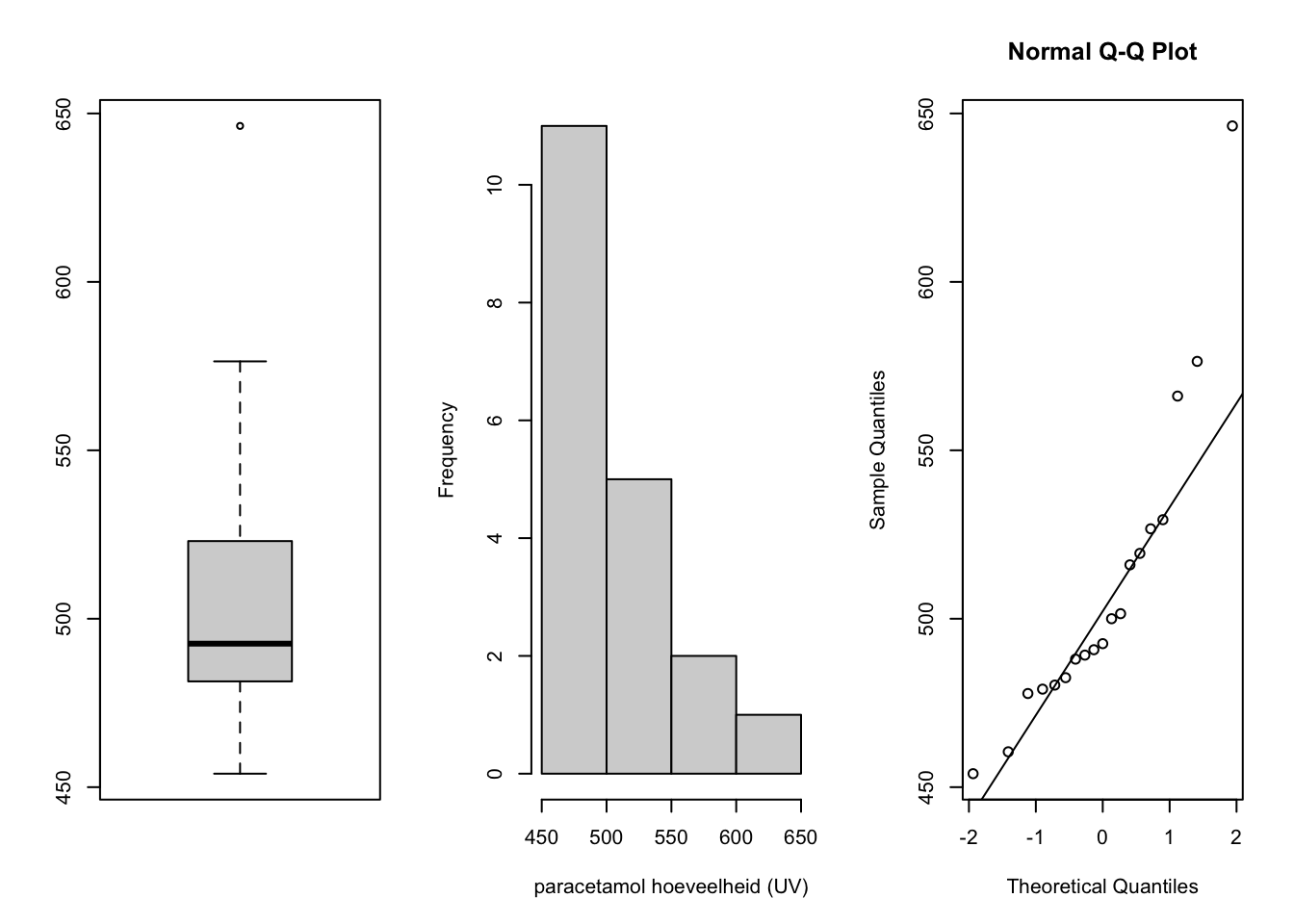
par(mfrow=c(1,1))
describe(d$Gem.UV)## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 19 509.29 45.87 492.6 504.49 21.94 454 646.3 192.3 1.45 1.78 10.52De hoeveelheid paracetamol is scheef verdeeld (rechtsscheef). Een logaritmische transformatie geeft een kleine verbetering, dat wil zeggen, de data zijn wat minder scheef, echter de scheefheid is niet geheel opgelost.
Je weet dat – bij een steekproef die groot genoeg is – het gemiddelde van deze gegevens wel een normale verdeling volgt (centrale limiet stelling). In deze dataset zitten gegevens over 19 tabletten. Niet erg groot – als grens voor het gebruik van de centrale limietstelling wordt vaak 30 genoemd - , maar voor een rechtsscheve verdeling groot genoeg. Je gaat dus de oorspronkelijke data voor de analyse gebruiken.
UV <- t.test(d$Gem.UV, mu = 500, alternative = "two.sided")
UV##
## One Sample t-test
##
## data: d$Gem.UV
## t = 0.88317, df = 18, p-value = 0.3888
## alternative hypothesis: true mean is not equal to 500
## 95 percent confidence interval:
## 487.1839 531.4056
## sample estimates:
## mean of x
## 509.2947Vraag 14. Wat is je conclusie ten aanzien van de onderzoeksvraag?
Stap 4 – Concludeer
De p-waarde is gelijk aan 0.3888. We verwerpen de nulhypothese dus niet.
De gemiddelde hoeveelheid paracetamol is niet significant verschillend
van 500 mg. Let op: dit is geen bewijs dat de gemiddelde hoeveelheid
paracetamol gelijk is aan 500 mg!
Vergeet niet je .R script op te slaan in een logische folder, zodat je deze voor je eigen data kan gebruiken.