In dit COO leer je gemiddelden en (95%) betrouwbaarheidsintervallen berekenen, en absorptie data plotten tegenover de concentraties van een antibioticum.
- Voorbereiding
- Betrouwbaarheidsintervallen (stap voor stap)
- 1.1 Data inlezen
- 1.2 Beschrijvende statistiek
- 1.3 Betrouwbaarheidsinterval voor een gemiddelde
- 1.4 Betrouwbaarheidsinterval voor het verschil tussen twee gemiddelden
- OD data inlezen en analyseren
0. Voorbereiding
Zorg er voor dat je de benodigde databestanden hebt gedownload en lokaal hebt opgeslagen:
Herhaling van COO2: open en sla dit bestand niet op met Excel (Windows) of Numbers (Mac). Zorg dat je de .csv bestanden meteen in de goede map opslaat, of verplaatst de bestanden zelf naar de juiste map zonder deze met Excel-achtige software te openen.
Het is ook handig om je ‘working directory’ te veranderen in deze map
met databestanden. Dit kun je doen via het menu: Session > Set
Working Directory > Choose Directory… > selecteer de map waarin de
databestanden staan. Let op tijdens het instellen van je ‘working
directory’ zie je de bestanden meestal niet staan. Of, je gebruikt
setwd().
Verder maken we gebruik van functies uit de psych
package. Als je die nog niet hebt geïnstalleerd, doe dat nu met de
functie install.packages(“psych”). Daarna kunnen we hem
inladen:
library(psych)1: Betrouwbaarheidsintervallen in R
In de zelfstudie is gekeken naar de optische densiteit (OD) bij een concentratie van het antibioticum van 250 mg/l. We gebruiken hier hetzelfde voorbeeld en kijken stap-voor-stap hoe we de data kunnen beschrijven, en hoe een 95% betrouwbaarheidsinterval (BHI) in R te laten berekenen.
1.1 Data inlezen
De data zijn opgeslagen in een het bestand OD250.csv. We
lezen de data in (voeg zelf de map toe waar je data staat als je geen
working directory hebt ingesteld) en we noemen de data frame
d1. We bekijken de eerste regels met head:
d1 <- read.csv("OD250.csv")dim(d1)## [1] 72 2head(d1)## stam OD250
## 1 1 0.091
## 2 2 0.369
## 3 3 0.488
## 4 4 0.563
## 5 5 0.313
## 6 6 0.3591.2 Beschrijvende statistiek
Vraag 1. Maak de side-by-side boxplot uit de zelfstudie van de OD bij 250 mg/l per stam. Zie COO4 als je niet meer weet hoe dit moet.
boxplot(OD250~ stam, data = d1, xlab="stam", ylab="OD")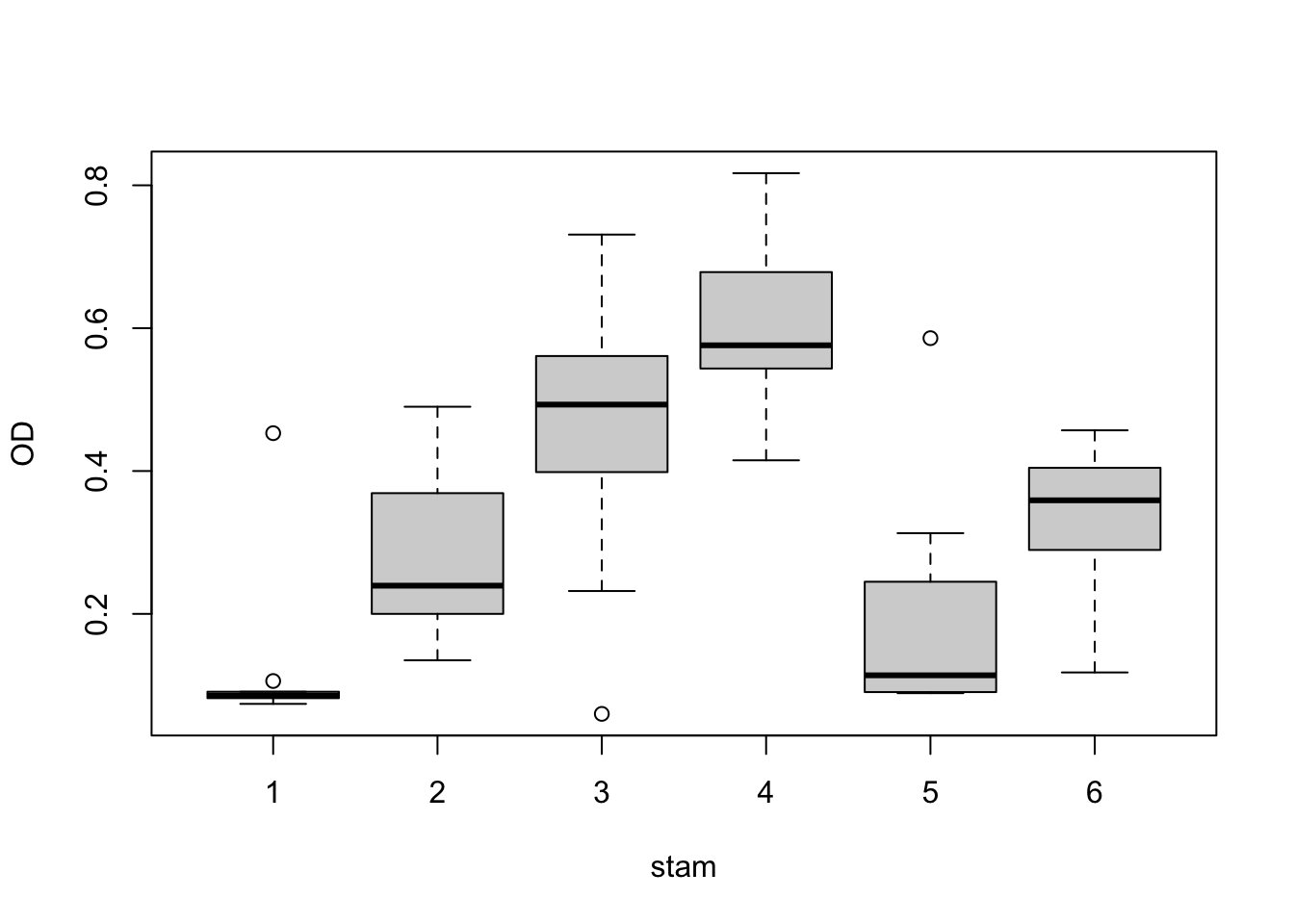
Om een gemiddelde OD en standaarddeviatie per stam te krijgen, kunnen
we steeds een selectie maken op de verschillende stammen en vragen om
die kengetallen. Veel makkelijker: we kunnen de
describeBy() functie gebruiken (we krijgen dan veel meer
dan mean en SD):
# Kerngetallen berekenen per stam
# skew = FALSE zorgt ervoor dat kerngetallen die ons niet interesseren niet geprint worden
describeBy(OD250 ~ stam, data = d1, skew = FALSE)##
## Descriptive statistics by group
## stam: 1
## vars n mean sd median min max range se
## OD250 1 12 0.12 0.11 0.09 0.07 0.45 0.38 0.03
## ----------------------------------------------------------------------------------------------------
## stam: 2
## vars n mean sd median min max range se
## OD250 1 12 0.28 0.11 0.24 0.14 0.49 0.36 0.03
## ----------------------------------------------------------------------------------------------------
## stam: 3
## vars n mean sd median min max range se
## OD250 1 12 0.46 0.18 0.49 0.06 0.73 0.67 0.05
## ----------------------------------------------------------------------------------------------------
## stam: 4
## vars n mean sd median min max range se
## OD250 1 12 0.61 0.12 0.58 0.42 0.82 0.4 0.03
## ----------------------------------------------------------------------------------------------------
## stam: 5
## vars n mean sd median min max range se
## OD250 1 12 0.18 0.15 0.11 0.09 0.59 0.5 0.04
## ----------------------------------------------------------------------------------------------------
## stam: 6
## vars n mean sd median min max range se
## OD250 1 12 0.33 0.1 0.36 0.12 0.46 0.34 0.03Vraag 2. Welke stam heeft de hoogste gemiddelde OD? Welke stam heeft de kleinste standaarddeviatie? En de grootste?
1.3 Betrouwbaarheidsinterval voor een gemiddelde
Laten we nu kijken naar stam 2. We hebben al een gemiddelde OD uitgerekend, wat is het 95% BHI voor de gemiddelde OD bij een concentratie van het antibioticum van 250 mg/l voor stam 2?
Vraag 3. Voor je het BHI uitrekent, kijk nogmaals naar de boxplot. Mogen we voor zo’n steekproef een BHI uitrekenen? Wat nemen we aan wanneer we dat doen?
We nemen aan dat de steekproef van metingen (1) aselecte is gekozen
uit (2) een populatie met een normale verdeling.
(1) De metingen zullen niet helemaal aselect gekozen zijn, omdat het
metingen van studenten uit hetzelfde vak betreft. Met zo’n experiment is
het bijna nooit zo dat waarnemingen helemaal onafhankelijk zijn,
laboraten zijn nooit aselect gekozen.
(2) Als de steekproef niet helemaal normaal verdeeld is, wil dat nog
niet zeggen dat de populatie niet normaal verdeeld is. En we
weten dat de centralelimietstelling zegt dat steekproefgemiddelden
normaal verdeeld zullen zijn rondom \(\mu\) wanneer de steekproef groot genoeg
is. Hier is de steekproef best klein (n=12), maar gelukkig geeft de
verdeling van de OD waardes geen reden om te twijfelen aan een normale
verdeling in de populatie. We mogen dus een BHI uitrekenen.
We gaan het toch doen. Om een 95% BHI (op basis van de t-verdeling)
uit te rekenen, maken we gebruik van de t-test() functie.
De t-toets wordt in Thema 3 behandeld, hier gebruiken we de functie
alleen voor het 95% BHI. We selecteren eerst een subset van de dataframe
door enkel de rijen te nemen waarin informatie voor stam 2 staan:
# Selecteer stam 2 data
stam2 <- d1[d1$stam == 2,]
# Bereken het 95% betrouwbaarheidsinterval
# De rest van de output negeren we
t.test(stam2$OD)##
## One Sample t-test
##
## data: stam2$OD
## t = 8.7514, df = 11, p-value = 2.755e-06
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.2077084 0.3472916
## sample estimates:
## mean of x
## 0.2775De gemiddelde OD is 0.277, met 95% BHI (0.208 – 0.347).
Vraag 4. Geef een interpretatie van dit BHI.
1.4 Betrouwbaarheidsinterval voor het verschil tussen twee gemiddelden
Stel dat we de optical density bij concentratie 250 mg/l willen
vergelijken tussen stammen twee en drie. Dan hebben we twee groepen van
metingen die we hier voor het gemak beschouwen als onafhankelijk van
elkaar (zie overpeinzingen in de zelfstudie). Is het verschil dat we in
de boxplot zien tussen de twee stammen een weerspiegeling van een
werkelijk verschil in de populaties (alle mogelijke OD metingen bij 250
mg/l for stammen 2 en 3), of zou dit verschil door toeval
(steekproefvariabiliteit) kunnen zijn onstaan? Om die vraag te
beantwoorden, kunnen we een 95% BHI voor het verschil in gemiddelden
uitrekenen. Daartoe maken we eerst een selectie van alleen die twee
stammen, en daarna gebruiken weer de t-test() functie.
# We selecteren nu rijen waarin informatie staat
# over stam 2 of (het | teken) stam 3
stam23 <- d1[d1$stam==2 | d1$stam==3,]
# We gebruiken hier een 'r formula' om aan te geven wat de groepen zijn
# in de test (stam23$stam). De waardes als input voor de test zijn de OD waarden (stam23$OD).
# Zie ?t.test voor meer info, onder 'formula'.
t.test(stam23$OD~stam23$stam)##
## Welch Two Sample t-test
##
## data: stam23$OD by stam23$stam
## t = -3.0595, df = 18.418, p-value = 0.006621
## alternative hypothesis: true difference in means between group 2 and group 3 is not equal to 0
## 95 percent confidence interval:
## -0.30930175 -0.05769825
## sample estimates:
## mean in group 2 mean in group 3
## 0.2775 0.4610Het verschil in gemiddelden in de steekproeven is 0.2775-0.461 = -0.184, met 95% BHI (-0.309 – -0.058).
Vraag 5a. Geef een interpretatie van dit BHI. Denk je dat er een verschil is in gemiddelden in de populatie?
Vraag 5b. Wat nemen we aan bij het uitrekenen van dit BHI? Voldoen de gegevens aan deze aannames?
Bij een BHI voor een verschil in twee onafhankelijke gemiddeldne nemen we aan dat de steekproeven (1) aselecte zijn gekozen uit (2) twee onafhankelijke populaties met (3) allebei een normale verdeling. (Let op: soms is er ook een vierde aanname, van gelijke varianties; daar gaan we in een latere cursus op in.)
- Alweer zullen de metingen niet helemaal aselect gekozen zijn, zie
vraag 3.
- De metingen hier zijn zo goed als zeker niet onafhankelijk van
elkaar: we hebben telkens van één student een OD voor stam 2 en een OD
voor stam 3. Waarschijnlijk lijken de metingen van de ene student meer
op elkaar dan metingen van verschillende studenten (de ene werkt
nauwkeuriger en netter dan de andere, bijvoorbeeld). Dan is een gepaarde
t-toets een betere optie. Daar gaan we ook in een latere cursus op
in.
- De steekproef van stam 3 is ook niet perfect normaal verdeeld, maar de verdeling van de OD waardes geeft geen reden om te twijfelen aan een normale verdeling in de populatie.
Al met al zijn de conclusies uit 5a. wellicht niet helemaal betrouwbaar, vooral door de schending van de tweede aanname.
2. OD data inlezen en analyseren
In het bestand ODdatavb.csv staan data van een
experiment zoals je zelf gaat uitvoeren: voor zes verschillende
bacteriestammen kijk je bij verschillende concentraties van een
antibioticum naar de groei(remming). De groei wordt uitgedrukt als OD.
Lees de data in en bekijk het:
OD.dat <-read.csv("OD-eigen-data-vb.csv", sep = ";")OD.dat## Concentratie stam1OD1 stam1OD2 stam1OD3 stam1OD4 stam2OD1 stam2OD2 stam2OD3 stam2OD4 stam3OD1 stam3OD2 stam3OD3 stam3OD4
## 1 c10 0.5676 0.5721 0.0731 0.7895 0.8288 0.4495 0.2596 0.6829 0.6073 0.9855 0.8426 0.66600
## 2 c50 0.2304 0.3814 0.0549 0.2330 0.5397 0.4095 0.3193 0.6058 0.5803 0.9423 0.7905 0.62800
## 3 c100 0.1103 0.3052 0.0526 0.1397 0.3992 0.3626 0.0490 0.5567 0.4768 0.7816 0.5747 0.66410
## 4 c250 0.0566 0.0673 0.0569 0.0613 0.2452 0.0586 0.0586 0.5376 0.2569 0.2838 0.2650 0.59335
## 5 c500 0.0499 0.0520 0.0997 0.0583 0.0745 0.0645 0.0541 0.4871 0.0794 0.1949 0.2907 0.42135
## 6 NegCont 0.1108 0.0489 0.0547 0.0455 0.0563 0.0489 0.0535 0.4524 0.0535 0.0489 0.4198 0.04440
## 7 PosCont1 0.6521 0.8136 0.5655 0.7447 0.9293 0.8152 0.6181 0.7486 0.7870 0.9263 0.8449 0.77470
## 8 PosCont2 0.7286 0.6495 0.7362 0.5945 0.6937 0.8123 0.8311 0.7577 0.8337 0.7921 0.8193 0.78970Let op: Dit bestand komt als het goed is volledig overeen met de structuur op de 96-wells platen die jullie gaan maken. De concentraties antibiotica worden in de rijen aangegeven, en in de kolommen staan steeds 4 herhalingen voor 3 verschillende stammen bacterien. Bij je eigen analyse en eigen data is het dus zaak om te zorgen voor precies dezelfde structuur als in dit document, anders zul je de code voor je eigen analyse zelf moeten aanpassen! Voor de analyse van je eigen data is het ook belangrijk dat zowel de variabelenamen (in de eerste rij van de .csv file) als de concentraties in de variabele “concentratie” slechts uit 1 woord bestaat.
Vraag 6. Bekijk de OD-waarden in het dataframe. Wellicht vallen je al een paar dingen op? Zijn er bijzonder hoge of bijzonder lage waarden van OD in de tabel? Welke waarden verwacht je ongeveer voor de negatieve controles? En welke waarden voor de positieve controles?
De waarden zien er best goed uit. Er zijn geen waarden boven 1 en er zijn geen negatieve waarden. We verwachten dat de negatieve controles rond 0.05 vallen, maar bij 2 observaties is dit beduidend hoger (0.45 en 0.42). De positieve controles zijn allemaal redelijk hoog, zoals je zou verwachten. Binnen de verdunningsreeksen zie je meestal dat de OD waarde flink afneemt bij hogere concentratie, hoewel dit niet altijd overtuigend is. Een aandachtspunt is kolom “stam1OD3”(3e herhaling van stam 1): hier zien we consequent lage OD waarden. Heeft de student hier soms vergeten om de bacterie toe te voegen? Let op! Deze lage waarden zijn op zichzelf geen reden om die te verwijderen uit je onderzoek. Wel zou het slim zijn om in het logboek te kijken of daar misschien iets fout is gegaan.
Omdat we per stam, per concentratie, 4 observaties hebben, kunnen we daar gemiddelden van berekenen, en op die manier met grotere precisie bepalen wat het gemiddelde in de populatie zal zijn voor die stam / concentratie combinatie.
De positieve controles hebben we zelfs in twee rijen, dus 8 keer gemeten. Deze 8 metingen zullen we gebruiken om per stam een gemiddelde met 95% BHI te berekenen, zodat we een goede schatting hebben van het populatie-gemiddelde van de OD waarde in die stam als er geen behandeling met antibiotica zou zijn.
De negatieve controles hebben we maar in 1 rij gemeten, maar in principe zijn alle negatieve controles - hoewel per stam gemeten - allemaal schatters voor hetzelfde, namelijk de OD bij een monster zonder bacteriën. Deze kunnen we dus ook middelen, en met een 95% BHI van het gemiddelde hebben we 95% zekerheid dat het BHI het werkelijke populatiegemiddelde van OD zonder infectie bevat.
Als het goed is zullen de (gemiddelden van) de OD waarden van met antibiotica behandelde bacteriele infecties ergens tussen die positieve en negatieve controles in vallen. Maar dit is een experiment, en daar kan natuurlijk vanalles fout gaan.
We gaan aan de slag met de data! Dat kan echter niet zomaar. De data staan nog niet zo geordend dat we meteen berekeningen uit kunnen voeren. We willen graag dat de variabelen in kolommen weergegeven worden in plaats van in rijen, en daarom moeten we deze data file zo herordenen dat de rijen kolommen worden en vice versa. Dat heet transponeren. De onderstaande code zorgt hiervoor. Daarna maken we nog een extra variabele die aangeeft van welke bacteriestam de data zijn. In dit code blok gebeurd veel, dus bekijk goed de tijdelijke tussenbestanden!
# Hier transponeren we de data.
# Ook laten we kolom 1 weg, omdat we die later toevoegen als kolomnamen (colnames)
tmp.dat1 <- OD.dat[,-1]
tmp.dat2 <- t(tmp.dat1)
# t() transponeert, maar maakt ook een matrix van je data.frame. Dit moeten we dus weer terugzetten
tmp.dat3 <- as.data.frame(tmp.dat2)
# We wijzen kolomnamen toe, we gebruiken de waardes die eerst in kolom 1 stonden.
colnames(tmp.dat3) <- OD.dat[,1]
# Nu maken we twee extra kolommen, met info over de stam en welke meeting het was.
# Controleer straks voor je eigen data goed of dit klopt!
tmp.dat3$Stam <- c(1,1,1,1,2,2,2,2,3,3,3,3)
tmp.dat3$Herhaling <- c(1,2,3,4,1,2,3,4,1,2,3,4)
# Onze nieuwe dataset
OD.dat.mod <- tmp.dat3Als je voor elke tussenstap snapt we er gebeurd, kun je de oude tussenbestanden verwijderen en verder gaan.
remove(tmp.dat1, tmp.dat2, tmp.dat3)Onze bewerkte (modified) data:
OD.dat.mod## c10 c50 c100 c250 c500 NegCont PosCont1 PosCont2 Stam Herhaling
## stam1OD1 0.5676 0.2304 0.1103 0.05660 0.04990 0.1108 0.6521 0.7286 1 1
## stam1OD2 0.5721 0.3814 0.3052 0.06730 0.05200 0.0489 0.8136 0.6495 1 2
## stam1OD3 0.0731 0.0549 0.0526 0.05690 0.09970 0.0547 0.5655 0.7362 1 3
## stam1OD4 0.7895 0.2330 0.1397 0.06130 0.05830 0.0455 0.7447 0.5945 1 4
## stam2OD1 0.8288 0.5397 0.3992 0.24520 0.07450 0.0563 0.9293 0.6937 2 1
## stam2OD2 0.4495 0.4095 0.3626 0.05860 0.06450 0.0489 0.8152 0.8123 2 2
## stam2OD3 0.2596 0.3193 0.0490 0.05860 0.05410 0.0535 0.6181 0.8311 2 3
## stam2OD4 0.6829 0.6058 0.5567 0.53760 0.48710 0.4524 0.7486 0.7577 2 4
## stam3OD1 0.6073 0.5803 0.4768 0.25690 0.07940 0.0535 0.7870 0.8337 3 1
## stam3OD2 0.9855 0.9423 0.7816 0.28380 0.19490 0.0489 0.9263 0.7921 3 2
## stam3OD3 0.8426 0.7905 0.5747 0.26500 0.29070 0.4198 0.8449 0.8193 3 3
## stam3OD4 0.6660 0.6280 0.6641 0.59335 0.42135 0.0444 0.7747 0.7897 3 4Om de data goed te beschrijven gaan we kijken naar:
- de OD waardes van de negatieve controles
- de OD waardes van de positieve controles
- de OD waardes van de observaties met verschillende concentraties antibiotica
Beantwoord nu op basis van OD.dat.mod de volgende vragen
over de OD-waarden van de negatieve controles.
Vraag 7. Beschrijf (getallen, plaatjes) de OD van de negatieve controles. Wat zie je?
boxplot(OD.dat.mod$NegCont)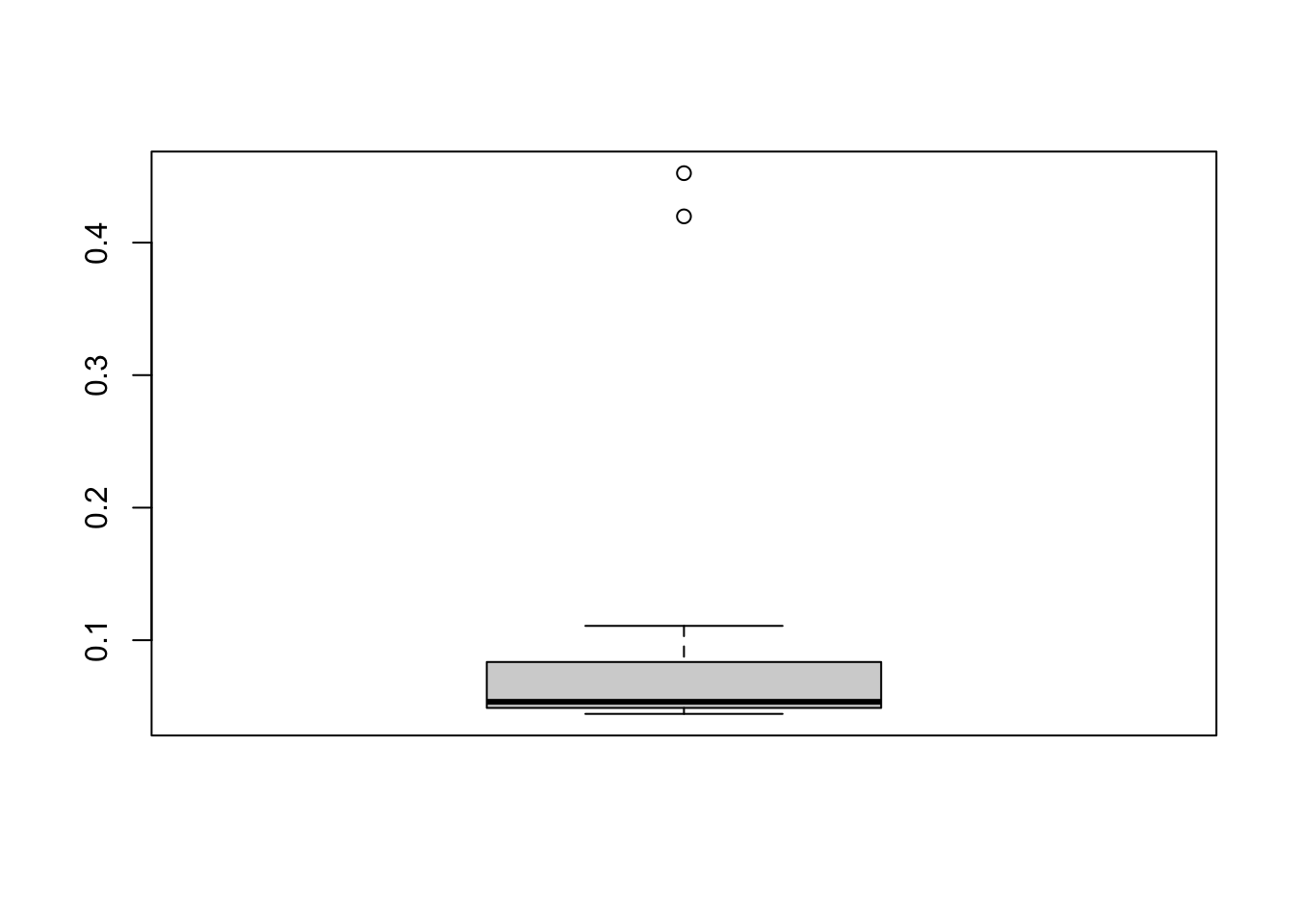
describe(OD.dat.mod$NegCont, na.rm=TRUE, skew=FALSE)## vars n mean sd median min max range se
## X1 1 12 0.12 0.15 0.05 0.04 0.45 0.41 0.04Door de uitschieters van 0.42 en 0.45 is de verdeling van de negatieve controles rechts-scheef. Verder hebben de waarden een best grote spreiding. (Als het experiment heel nauwkeurig wordt gedaan door iemand met veel ervaring, zouden we allemaal negatieve controles rond de 0.05 verwachten, en in ieder geval onder de 0.1.)
Vraag 8. Wat is het 95% BHI voor de gemiddelde OD van de negatieve controles in dit experiment?
t.test(OD.dat.mod$NegCont)##
## One Sample t-test
##
## data: OD.dat.mod$NegCont
## t = 2.7861, df = 11, p-value = 0.01771
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.02516084 0.21443916
## sample estimates:
## mean of x
## 0.1198Vraag 9. Wat vind je van het gemiddelde OD voor de negatieve controles?
Het gemiddelde is, mede door de hoge uitschieter, best hoog. De overige controles zitten bijna allemaal rond 0.05, maar de uitschieters halen het gemiddelde (vooral op zo’n kleine steekproef) flink omhoog.
Vraag 10. Wat vind je van de breedte het 95% BHI van het gemiddelde negatieve controle? Hoe zouden we het interval smaller kunnen krijgen?
Door de grote spreiding in de negatieve controles en door de kleine
steekproef (n=12) is de standaardfout van het gemiddelde groter dan we
zouden willen, en het BHI dus breder dan we zouden willen.
Door èn nauwkeuriger te werken èn een grotere steekproef te nemen van de
negatieve controles, zou je meer precisie moeten krijgen: een kleinere
SE en een smaller BHI, dus meer zekerheid over de OD wanneer er geen
bacterie in het welletje zit.
Het is handig om het gemiddelde en de uiteinden van het BHI van de
negatieve controle op te slaan voor de plot. We halen de onder- en
bovengrens (elementen [1] en [2] van de conf.int) uit het
object dat gemaakt wordt door de t.test() functie.
Neg.mean <- mean(OD.dat.mod$NegCont)
# Confidence interval
Output.ttest <- t.test(OD.dat.mod$NegCont) # Je ziet dat dit een list is met 10 elementen
# In het element 'conf.int' zit een vector met twee waardes
Neg.ll <- Output.ttest$conf.int[1] # De lower limit (ll)
Neg.ul <- Output.ttest$conf.int[2] # De upper limit (ul)Hoe kun je checken of dit gelukt is?
Dezelfde vragen gaan we nu beantwoorden over de OD-waarden van de positieve controles. Maar daar is eerst weer een bewerking van de data voor nodig. Per stam en herhaling heb je twee positieve controle metingen gedaan. Deze metingen staan nu nog in twee kolommen. Voor je analyse is het makkelijker als je de positieve metingen allemaal in dezelfde kolom hebt. Dit regel je met “reshape”, een functie die van een ‘wide’, naar een ‘long’ format gaat. Je kunt daarvoor de onderstaande code gebruiken. Let op: ook als ervaren R-gebruiken is dit vaak even uitproberen. Als je dit zelf gaat doen is het niet gek als je dit een paar keer moet proberen, tot dat je de indeling hebt die je wilt.
stam1 <- OD.dat.mod[OD.dat.mod$Stam==1,] # Eerst selecteren we alleen de gegevens van stam 1
stam1 # wide## c10 c50 c100 c250 c500 NegCont PosCont1 PosCont2 Stam Herhaling
## stam1OD1 0.5676 0.2304 0.1103 0.0566 0.0499 0.1108 0.6521 0.7286 1 1
## stam1OD2 0.5721 0.3814 0.3052 0.0673 0.0520 0.0489 0.8136 0.6495 1 2
## stam1OD3 0.0731 0.0549 0.0526 0.0569 0.0997 0.0547 0.5655 0.7362 1 3
## stam1OD4 0.7895 0.2330 0.1397 0.0613 0.0583 0.0455 0.7447 0.5945 1 4# Om naar long te gaan gebruiken we reshape.
# Bekijk ook ?reshape
od.posS1 <- reshape(stam1, # Onze input df
idvar=c("Stam", "Herhaling"), # De id kolommen voor individuele metingen
varying=c("PosCont1", "PosCont2"), # De kolommen met de waardes die we onder elkaar willen
v.names = "OD", # De naam die we geven aan de nieuwe kolom met waardes onder elkaar
direction="long", # We willen naar een 'long' format
times=c("PosCont1", "PosCont2"), # De twee kolommen waar de metingen van de positieve controles in staan
drop=c("c500", "c250", "c100", "c50", "c10","NegCont") # De kolommen die we niet mee willen nemen
)
od.posS1 # long, vergelijk alle waarden: staan die allemaal op de goede plaats?## Stam Herhaling time OD
## 1.1.PosCont1 1 1 PosCont1 0.6521
## 1.2.PosCont1 1 2 PosCont1 0.8136
## 1.3.PosCont1 1 3 PosCont1 0.5655
## 1.4.PosCont1 1 4 PosCont1 0.7447
## 1.1.PosCont2 1 1 PosCont2 0.7286
## 1.2.PosCont2 1 2 PosCont2 0.6495
## 1.3.PosCont2 1 3 PosCont2 0.7362
## 1.4.PosCont2 1 4 PosCont2 0.5945Nu kunnen we onderstaande vragen beantwoorden.
Vraag 11. Beschrijf (getallen, plaatjes) de OD van de positieve controles voor de eerste stam. Wat zie je?
boxplot(od.posS1$OD)
describe(od.posS1$OD, na.rm=TRUE, skew=FALSE)## vars n mean sd median min max range se
## X1 1 8 0.69 0.08 0.69 0.57 0.81 0.25 0.03Vraag 12. Wat is het 95% BHI voor de gemiddelde OD van de positieve controles van stam 1 in dit experiment?
t.test(od.posS1$OD)##
## One Sample t-test
##
## data: od.posS1$OD
## t = 23.075, df = 7, p-value = 7.28e-08
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.6153313 0.7558437
## sample estimates:
## mean of x
## 0.6855875Vraag 13. Wat vind je van het gemiddelde en de breedte het 95% BHI van de positieve controles van stam 1?
Dit ziet er goed uit.
Stam 1: 0.69 (0.62-0,76)
Overigens, voor de andere twee stammen geldt: Stam 2: 0.77 (0.70-0.85) Stam 3: 0.82 (0.78-0.86). de positieve controles van stam 3 hebben 1 hoge uitbijter. Daardoor is dit gemiddelde en BHI vrij hoog.
Ook het gemiddelde en de uiteinden van het BHI van de positieve controle slaan we op voor de plot. Dit kan met onderstaande code:
PosS1.mean <- mean(od.posS1$OD)
PosS1.ll <- t.test(od.posS1$OD)$conf.int[1]
PosS1.ul <- t.test(od.posS1$OD)$conf.int[2]Herhaal bovenstaande voor de positieve controles van stammen 2 en 3.
Als laatste gaan we nu per stam een grafiek maken waarin de OD waarden van verschillende concentraties gevisualiseerd worden.
Om grafieken te maken per stam, starten we weer met de datafile
OD.dat.mod, en moeten we de data weer omvormen. De gegevens staan nu
weer in het ‘wide format’, met één regel per stam, maar om een grafiek
te krijgen van OD per concentratie moeten we één regel per concentratie
per stam en per herhaling hebben (‘long format’). We gebruiken dus weer
de reshape() functie. Omdat deze functie meestal wordt
gebruikt bij longitudinale data, heet de optie om de verschillende
regels per concentratie te maken ‘times’. Dat is wellicht verwarrend,
‘time’ is in dit geval dus concentratie. Als we kijken naar de
resulterend data frame, dan zien we dat het handig is om de tweede
variabele te hernoemen. Dat doen we met colnames().
od.long <- reshape(OD.dat.mod, # Input df
idvar=c("Stam","Herhaling"), # Variabele om de verschillende meetingen uit elkaar te houden
varying=list(1:5), # De kolommen met OD waardes, we gebruiken nu numerieke indexen ipv kolom namen
v.names = "OD", # Naam van de nieuwe kolom met OD waardes
direction="long",
times=c(10, 50, 100, 250, 500), # Let op dat deze volgorde klopt voor je eigen data
drop=c("NegCont","PosCont1","PosCont2") # Deze kolommen willen we niet meenemen
)
colnames(od.long) <- c("Stam", "Herhaling", "conc", "OD") # Nodig om variabele "times"te hernoemen naar "conc"
head(od.long)## Stam Herhaling conc OD
## 1.1.10 1 1 10 0.5676
## 1.2.10 1 2 10 0.5721
## 1.3.10 1 3 10 0.0731
## 1.4.10 1 4 10 0.7895
## 2.1.10 2 1 10 0.8288
## 2.2.10 2 2 10 0.4495Nu kunnen we een plot maken per stam van OD vs. concentratie. We doen hier stam 1.
st1 <- od.long[od.long$Stam==1,]
st1 #check## Stam Herhaling conc OD
## 1.1.10 1 1 10 0.5676
## 1.2.10 1 2 10 0.5721
## 1.3.10 1 3 10 0.0731
## 1.4.10 1 4 10 0.7895
## 1.1.50 1 1 50 0.2304
## 1.2.50 1 2 50 0.3814
## 1.3.50 1 3 50 0.0549
## 1.4.50 1 4 50 0.2330
## 1.1.100 1 1 100 0.1103
## 1.2.100 1 2 100 0.3052
## 1.3.100 1 3 100 0.0526
## 1.4.100 1 4 100 0.1397
## 1.1.250 1 1 250 0.0566
## 1.2.250 1 2 250 0.0673
## 1.3.250 1 3 250 0.0569
## 1.4.250 1 4 250 0.0613
## 1.1.500 1 1 500 0.0499
## 1.2.500 1 2 500 0.0520
## 1.3.500 1 3 500 0.0997
## 1.4.500 1 4 500 0.0583plot(
st1$OD ~ st1$conc, # y ~ x
pch = 19,
main = "Stam 1",
ylab = "OD",
xlab = "concentratie AB"
)
Vraag 14. Beschrijf de relatie tussen OD en concentratie van het antibioticum. Lijkt het alsof stam 1 gevoelig is voor het AB?
Als laatste combineren we alle gegevens. We voegen lijnen toe aan het
plaatje voor het gemiddelde en 95% BHI van de positieve en van de
negatieve controles. Waarom moeten we nu de grenzen van de y-as
veranderen? Snap je wat we doen om de lowest en
highest Y waarde te vinden?
# Kleinste getal in Y data of BHI limieten
lowest <- min(c(st1$OD, Neg.ll, Neg.ul, PosS1.ul, PosS1.ll))
# Hoogste getal in Y data of BHI limieten
highest <- max(c(st1$OD, Neg.ll, Neg.ul, PosS1.ul, PosS1.ll))
# Basis plot met punten
plot(
st1$OD ~ st1$conc, # y ~ x
ylim = c(lowest - 0.1, highest + 0.1),
pch = 19,
main = "Stam 1",
ylab = "OD",
xlab = "concentratie AB"
)
# Lijnen voor positieve controles
abline(h=PosS1.mean, col="green") # Mean
abline(h=PosS1.ll, col="green", lty=2) # Lower limit
abline(h=PosS1.ul, col="green", lty=2) # Upper limit
# Lijnen voor negatieve controles
abline(h=Neg.mean, col="red")
abline(h=Neg.ll, col="red", lty=2)
abline(h=Neg.ul, col="red", lty=2)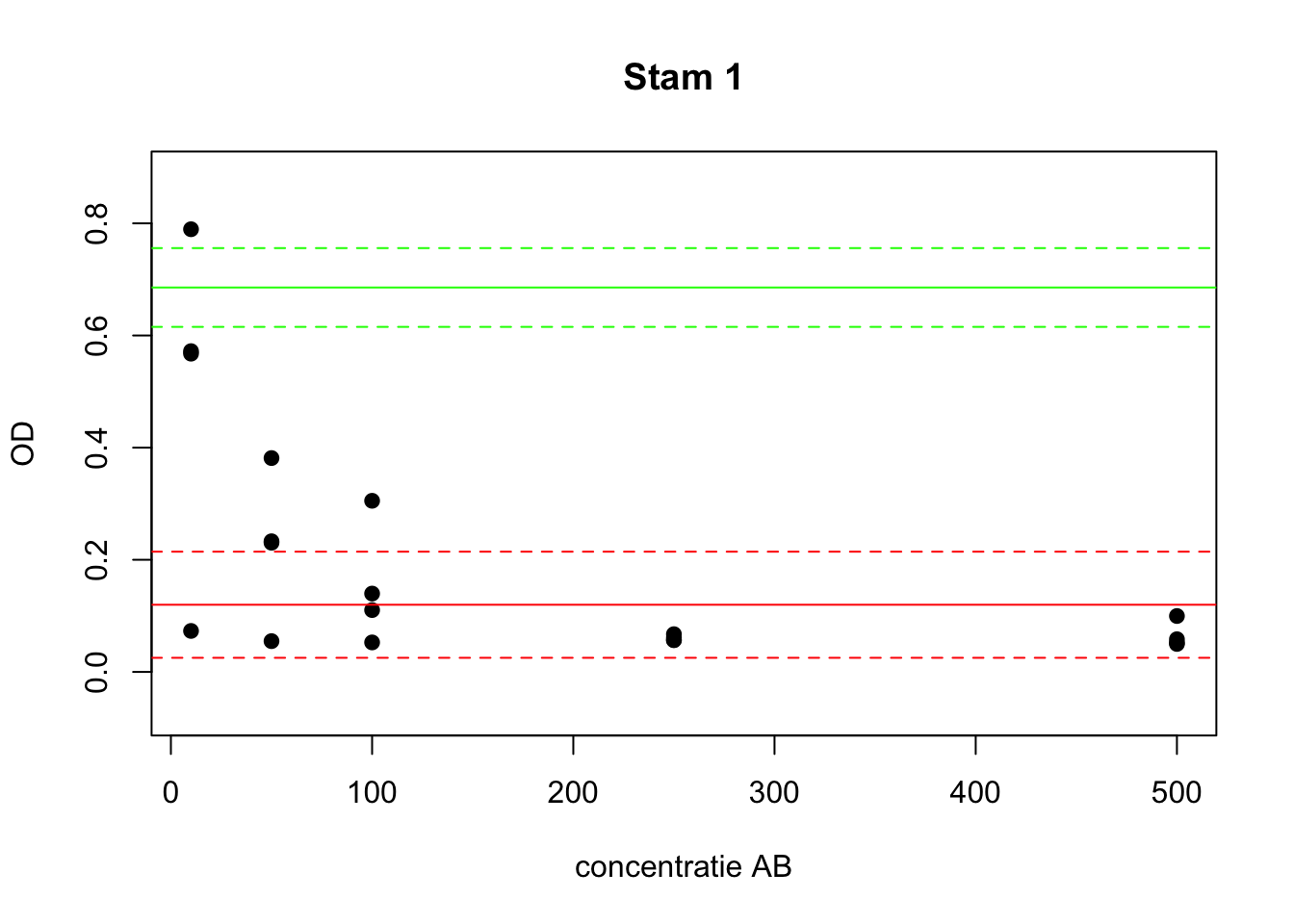
Vraag 15. Als we groeiremming definiëren als ‘OD lager dan de bovengrens van het 95% BHI van de negatieve controles’, wat moeten we concluderen bij stam 1?
Vraag 16. Herhaal het plaatje voor stammen 2 en 3 en trek conclusies.
stam2 <- OD.dat.mod[OD.dat.mod$Stam==2,]
stam2 #check## c10 c50 c100 c250 c500 NegCont PosCont1 PosCont2 Stam Herhaling
## stam2OD1 0.8288 0.5397 0.3992 0.2452 0.0745 0.0563 0.9293 0.6937 2 1
## stam2OD2 0.4495 0.4095 0.3626 0.0586 0.0645 0.0489 0.8152 0.8123 2 2
## stam2OD3 0.2596 0.3193 0.0490 0.0586 0.0541 0.0535 0.6181 0.8311 2 3
## stam2OD4 0.6829 0.6058 0.5567 0.5376 0.4871 0.4524 0.7486 0.7577 2 4od.posS2 <- reshape(stam2, idvar="Herhaling", varying=list(9:10), v.names = "OD",
direction="long", times=c("PosCont1", "PosCont2"),
drop=c("c500", "c250", "c100", "c50", "c10","NegCont"))
od.posS2## PosCont1 PosCont2 time OD
## 1.PosCont1 0.9293 0.6937 PosCont1 2
## 2.PosCont1 0.8152 0.8123 PosCont1 2
## 3.PosCont1 0.6181 0.8311 PosCont1 2
## 4.PosCont1 0.7486 0.7577 PosCont1 2
## 1.PosCont2 0.9293 0.6937 PosCont2 1
## 2.PosCont2 0.8152 0.8123 PosCont2 2
## 3.PosCont2 0.6181 0.8311 PosCont2 3
## 4.PosCont2 0.7486 0.7577 PosCont2 4st2 <- od.long[od.long$Stam==2,]
st2 #check## Stam Herhaling conc OD
## 2.1.10 2 1 10 0.8288
## 2.2.10 2 2 10 0.4495
## 2.3.10 2 3 10 0.2596
## 2.4.10 2 4 10 0.6829
## 2.1.50 2 1 50 0.5397
## 2.2.50 2 2 50 0.4095
## 2.3.50 2 3 50 0.3193
## 2.4.50 2 4 50 0.6058
## 2.1.100 2 1 100 0.3992
## 2.2.100 2 2 100 0.3626
## 2.3.100 2 3 100 0.0490
## 2.4.100 2 4 100 0.5567
## 2.1.250 2 1 250 0.2452
## 2.2.250 2 2 250 0.0586
## 2.3.250 2 3 250 0.0586
## 2.4.250 2 4 250 0.5376
## 2.1.500 2 1 500 0.0745
## 2.2.500 2 2 500 0.0645
## 2.3.500 2 3 500 0.0541
## 2.4.500 2 4 500 0.4871PosS2.mean <- mean(od.posS2$OD)
PosS2.ll <- t.test(od.posS2$OD)$conf.int[1]
PosS2.ul <- t.test(od.posS2$OD)$conf.int[2]
# Kleinste getal in Y data of BHI limieten
lowest <- min(c(st2$OD, Neg.ll, Neg.ul, PosS2.ul, PosS2.ll))
# Hoogste getal in Y data of BHI limieten
highest <- max(c(st2$OD, Neg.ll, Neg.ul, PosS2.ul, PosS2.ll))
plot(st2$OD ~ st2$conc, ylim=c(lowest-0.1,highest+0.1), pch=19,
main="Stam 2", ylab="OD", xlab="concentratie AB")
abline(h=PosS2.mean, col="green")
abline(h=PosS2.ll, col="green", lty=2)
abline(h=PosS2.ul, col="green", lty=2)
abline(h=Neg.mean, col="red")
abline(h=Neg.ll, col="red", lty=2)
abline(h=Neg.ul, col="red", lty=2)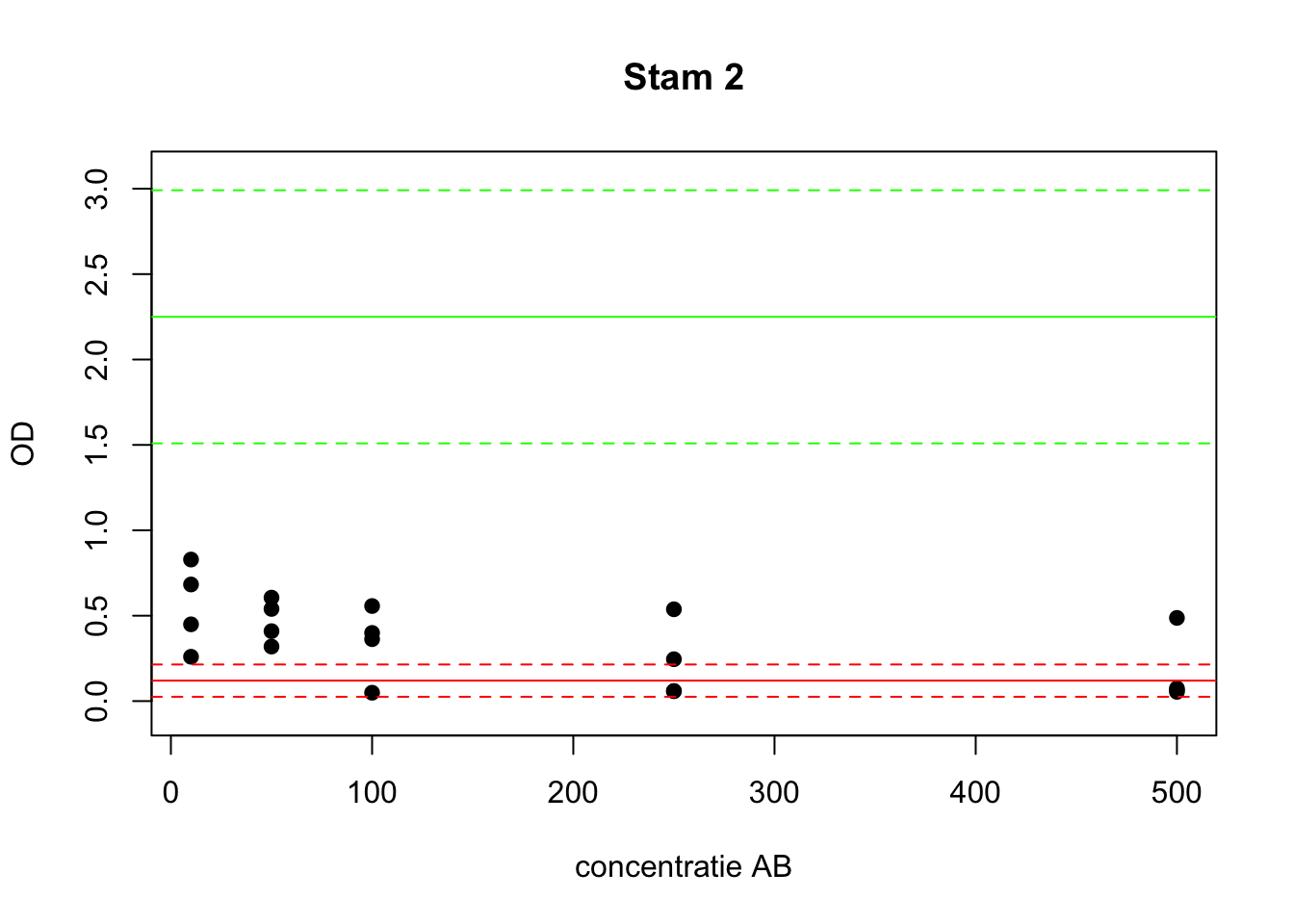
Bij stam 2 zien we dat er een grote spreiding is in de 3 waarden per concentratie AB. Er is misschien een dalende trend, want bij de laagste concentratie zijn er al lagere OD waardes die onder de ondergrens van de positieve controles vallen, maar daarna is er een nauwelijks een dalende trend in OD.De waardes komen niet consequent onder de bovengrens van de negatieve controles en daarom is het moeilijk om een goede conclusie te trekken.
stam3 <- OD.dat.mod[OD.dat.mod$Stam==3,]
stam3 #check## c10 c50 c100 c250 c500 NegCont PosCont1 PosCont2 Stam Herhaling
## stam3OD1 0.6073 0.5803 0.4768 0.25690 0.07940 0.0535 0.7870 0.8337 3 1
## stam3OD2 0.9855 0.9423 0.7816 0.28380 0.19490 0.0489 0.9263 0.7921 3 2
## stam3OD3 0.8426 0.7905 0.5747 0.26500 0.29070 0.4198 0.8449 0.8193 3 3
## stam3OD4 0.6660 0.6280 0.6641 0.59335 0.42135 0.0444 0.7747 0.7897 3 4od.posS3 <- reshape(stam3, idvar="Herhaling", varying=list(9:10), v.names = "OD",
direction="long", times=c("PosCont1", "PosCont2"),
drop=c("c500", "c250", "c100", "c50", "c10","NegCont"))
od.posS3## PosCont1 PosCont2 time OD
## 1.PosCont1 0.7870 0.8337 PosCont1 3
## 2.PosCont1 0.9263 0.7921 PosCont1 3
## 3.PosCont1 0.8449 0.8193 PosCont1 3
## 4.PosCont1 0.7747 0.7897 PosCont1 3
## 1.PosCont2 0.7870 0.8337 PosCont2 1
## 2.PosCont2 0.9263 0.7921 PosCont2 2
## 3.PosCont2 0.8449 0.8193 PosCont2 3
## 4.PosCont2 0.7747 0.7897 PosCont2 4st3 <- od.long[od.long$Stam==3,]
st3 #check## Stam Herhaling conc OD
## 3.1.10 3 1 10 0.60730
## 3.2.10 3 2 10 0.98550
## 3.3.10 3 3 10 0.84260
## 3.4.10 3 4 10 0.66600
## 3.1.50 3 1 50 0.58030
## 3.2.50 3 2 50 0.94230
## 3.3.50 3 3 50 0.79050
## 3.4.50 3 4 50 0.62800
## 3.1.100 3 1 100 0.47680
## 3.2.100 3 2 100 0.78160
## 3.3.100 3 3 100 0.57470
## 3.4.100 3 4 100 0.66410
## 3.1.250 3 1 250 0.25690
## 3.2.250 3 2 250 0.28380
## 3.3.250 3 3 250 0.26500
## 3.4.250 3 4 250 0.59335
## 3.1.500 3 1 500 0.07940
## 3.2.500 3 2 500 0.19490
## 3.3.500 3 3 500 0.29070
## 3.4.500 3 4 500 0.42135PosS3.mean <- mean(od.posS3$OD)
PosS3.ll <- t.test(od.posS3$OD)$conf.int[1]
PosS3.ul <- t.test(od.posS3$OD)$conf.int[2]
# Kleinste getal in Y data of BHI limieten
lowest <- min(c(st3$OD, Neg.ll, Neg.ul, PosS3.ul, PosS3.ll))
# Hoogste getal in Y data of BHI limieten
highest <- max(c(st3$OD, Neg.ll, Neg.ul, PosS3.ul, PosS3.ll))
plot(st3$OD ~ st3$conc, ylim=c(lowest-0.1, highest+0.1), pch=19,
main="Stam 3", ylab="OD", xlab="concentratie AB")
abline(h=PosS3.mean, col="green")
abline(h=PosS3.ll, col="green", lty=2)
abline(h=PosS3.ul, col="green", lty=2)
abline(h=Neg.mean, col="red")
abline(h=Neg.ll, col="red", lty=2)
abline(h=Neg.ul, col="red", lty=2)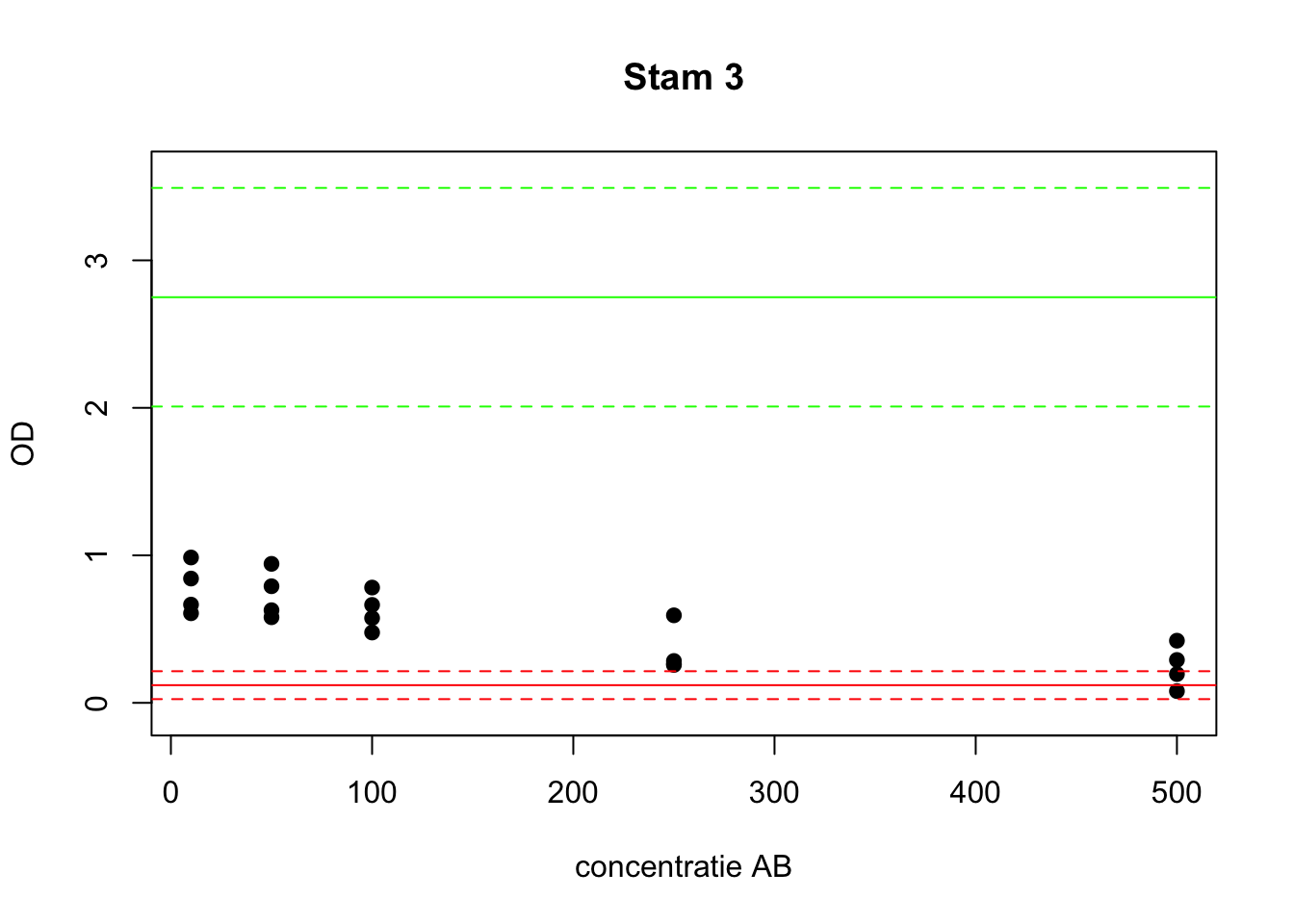
Bij stam 3 zien we weer een duidelijkere dalende trend in OD. Wel zien we dat er bij bijna alle concentraties een OD is die hoger is dan de bovengrens van het 95% BHI, behalve bij de hoogste concentratie AB. We concluderen dat er pas bij een hoge concentratie AB groeiremming is; stam 3 is matig gevoelig voor dit AB.
Vraag 17a. Stel dat we de negatieve controles zouden gebruiken van alle studenten die het practicum doen. Hoe zal dit de grenzen van het 95% BHI beïnvloeden?
Vraag 17b. Er zijn twee belangrijke aannames voor het berekenen van een BHI. Hoe denk je dat het zit met deze twee aannames met de negatieve controles wanneer we data gebruiken van alle studenten?
Vergeet niet je .R script op te slaan in een logische folder, zodat je deze voor je eigen data kan gebruiken.